10:15
Two exact solutions in the theory of biogenic mixing by microorganisms
Abstract
Suspensions of active particles, such as swimming microorganisms, turn out to be efficient stirrers of the surrounding fluid. This fact may be directly relevant to the feeding and evolutionary strategies of swimming cells. Microfluidic devices exploring swimmers-induced mixing have been proposed. The possibility of a significant biogenic contribution to the ocean circulation is currently under intense debate. However, understanding fluctuations and the effective tracer diffusion in these non-equilibrium systems remains a challenge.
In this talk we focus on the fundamentals of these processes. We discuss the impediments to stirring by force-free microswimmers and give a classification of the possible stirring mechanisms. We show that enhanced mixing may arise due to entrainment of the surrounding fluid by individual swimmers moving on infinite straight trajectories. Our first exact result shows that the total amount of fluid entrained by a swimmer, also know as its Darwin drift, is finite and can be decomposed into a universal and model-dependent parts that have a clear physical meaning.
A different stirring mechanism arises for swimmers having curved trajectories. We show that the previously suggested model of swimmers moving in straight finite runs interspersed with random reorientations can be solved exactly. In particular, we calculate the effective tracer diffusion coefficient for a suspension of dipolar swimmers and show that swimmers confined to a plane give rise to a Levy flight process.
Our results provide a quantitative description of the enhanced tracer mixing in dilute suspensions of microswimmers. They agree with the results of numerical simulations and recent experiments with suspension of E. coli.


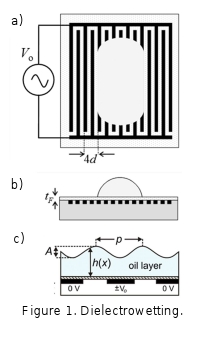 The contact angle of a
liquid droplet on a surface can be controlled by making the droplet part of a
capacitive structure where the droplet contact area forms one electrode to
create an electrowetting-on-dielectric (EWOD) configuration [1]. EWOD
introduces a capacitive energy associated with the charging of the solid-liquid
interface, in addition to the surface free energy, to allow the contact angle,
and hence effective hydrophilicity of a surface, to be controlled using a voltage.
However, the substrate must include an electrode coated with a thin, and
typically hydrophobic, solid insulating layer and the liquid must be
conducting, typically a salt solution, and have a direct electrical contact. In
this seminar I show that reversible voltage programmed control of droplet
wetting of a surface can be achieved using non-conducting dielectric liquids
and without direct electrical contact. The approach is based on non-uniform
electric fields generated via interdigitated electrodes and liquid
dielectrophoresis to alter the energy balance of a droplet on a solid surface
(Fig. 1a,b). Data is shown for thick droplets demonstrating the change in the
cosine of the contact angle is proportional to the square of the applied
voltage and it is shown theoretically why this equation, similar to that found
for EWOD can be expected [2]. I also show that as the droplet spreads and
becomes a film, the dominant change in surface free energy to be expected occurs
by a wrinkling/undulation of the liquid-vapor interface (Fig. 1c) [3,4]. This
type of wrinkle is shown to be a method to create a voltage programmable phase
grating [5]. Finally, I argue that dielectrowetting can be used to modify the
dynamic contact angle observed during droplet spreading and that this is
described by a modified form of the Hoffman-de Gennes law for the relationship
between edge speed and contact angle. In this dynamic situation, three distinct
regimes can be predicted theoretically and are observed experimentally. These
correspond to an exponential approach to equilibrium, a pure Tanner’s law type
power law and a voltage determined superspreading power law behavior [6].
The contact angle of a
liquid droplet on a surface can be controlled by making the droplet part of a
capacitive structure where the droplet contact area forms one electrode to
create an electrowetting-on-dielectric (EWOD) configuration [1]. EWOD
introduces a capacitive energy associated with the charging of the solid-liquid
interface, in addition to the surface free energy, to allow the contact angle,
and hence effective hydrophilicity of a surface, to be controlled using a voltage.
However, the substrate must include an electrode coated with a thin, and
typically hydrophobic, solid insulating layer and the liquid must be
conducting, typically a salt solution, and have a direct electrical contact. In
this seminar I show that reversible voltage programmed control of droplet
wetting of a surface can be achieved using non-conducting dielectric liquids
and without direct electrical contact. The approach is based on non-uniform
electric fields generated via interdigitated electrodes and liquid
dielectrophoresis to alter the energy balance of a droplet on a solid surface
(Fig. 1a,b). Data is shown for thick droplets demonstrating the change in the
cosine of the contact angle is proportional to the square of the applied
voltage and it is shown theoretically why this equation, similar to that found
for EWOD can be expected [2]. I also show that as the droplet spreads and
becomes a film, the dominant change in surface free energy to be expected occurs
by a wrinkling/undulation of the liquid-vapor interface (Fig. 1c) [3,4]. This
type of wrinkle is shown to be a method to create a voltage programmable phase
grating [5]. Finally, I argue that dielectrowetting can be used to modify the
dynamic contact angle observed during droplet spreading and that this is
described by a modified form of the Hoffman-de Gennes law for the relationship
between edge speed and contact angle. In this dynamic situation, three distinct
regimes can be predicted theoretically and are observed experimentally. These
correspond to an exponential approach to equilibrium, a pure Tanner’s law type
power law and a voltage determined superspreading power law behavior [6].