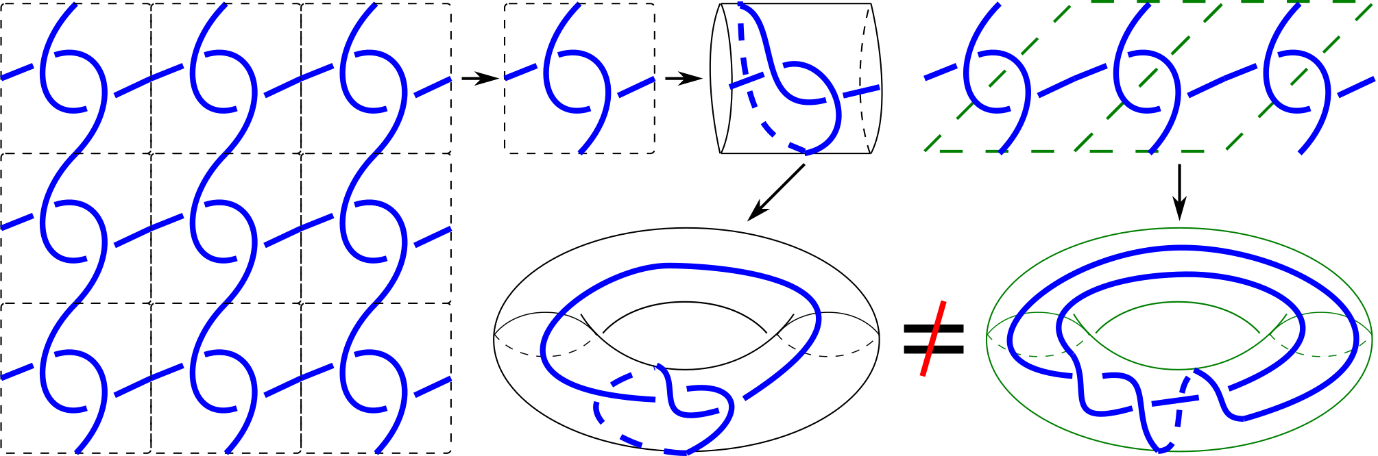Periodic Geometry and Topology for Materials Science

By Vitaly Kurlin

Liverpool’s team working on WP2 (applications to materials) develops the new area of Periodic Geometry and Topology to continuously parameterize the space of all potential crystals.

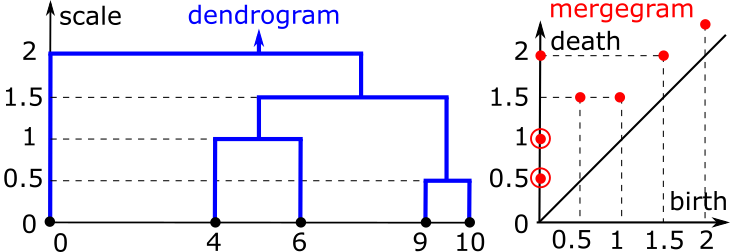
The first major result within the TDA grant is the extension of a Homologically Persistent Skeleton to higher dimensions [1]. The more recent contribution to the TDA is the mergegram [2] that maps any dendrogram hierarchical clustering into a diagram of pairs (birth,death) representing the life span of any intermediate cluster, not only the clusters that start from scale 0 as in 0-dimensional persistence.

The collaboration with chemists at the Materials Innovation Factory led by the co-I Prof Andy Cooper FRS has helped our group to establish the new area of Periodic Geometry and Topology, see the introductihon at the first conference MACSMIN: Maths and Computer Science for Materials Innovation.

Solid crystalline materials (periodic crystals) can have many types, all consist of elementary blocks (motifs) of atoms, ions or molecules in a unit cell periodically repeated in 3 directions.

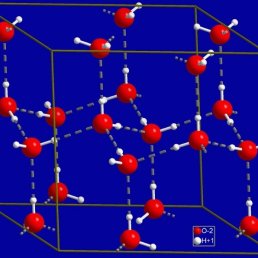
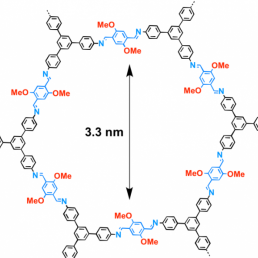
The above picture on the left shows hexagonal cycles of water molecules in solid ice, the picture on the right shows a complicated hexagonal cycle of molecules in a periodic metal organic framework.

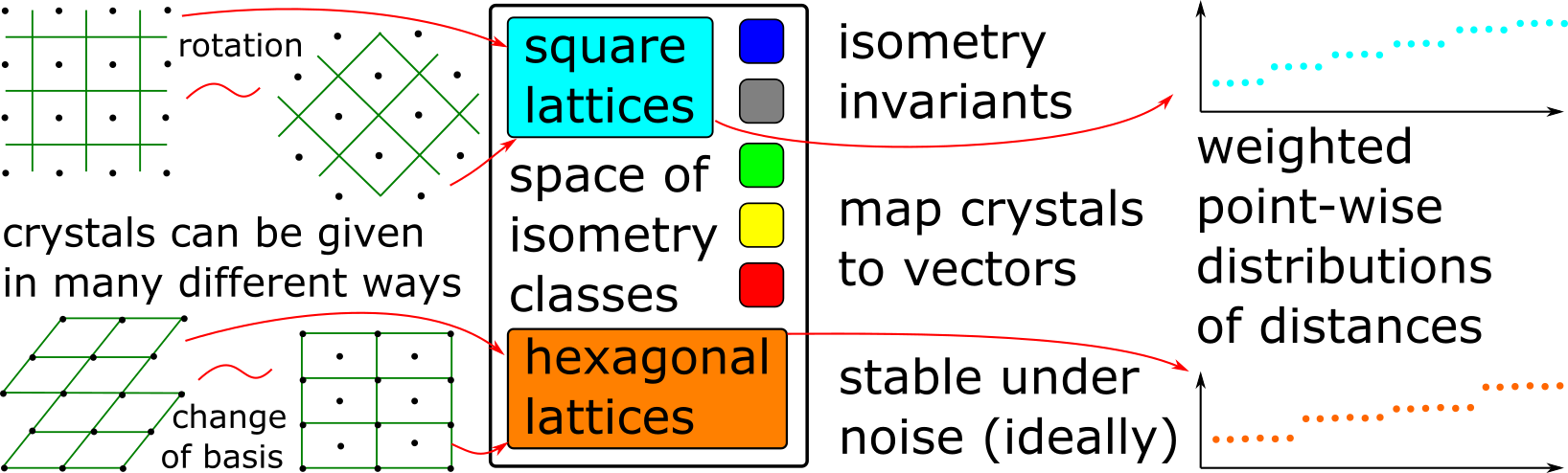
The key problem in materials discovery is the curse of ambiguity meaning that the same periodic structure can be represented by infinitely many different combinations of a unit cell and a motif.

The example of 2-periodic textiles [3] shows that fixing a unit cell makes equivalent periodic structures different in a fixed torus. Similarly, all crystal invariants should be independent of a unit cell.

Since most solid crystals are rigid, they should be considered modulo rigid motions or isometries that preserve interpoint distances. Mathematically, a crystal is the isometry class of periodic points sets modulo changes of a basis and isometries. The isometry classification of crystals should include the extra condition of stability under perturbations of points. Indeed, atoms vibrate above the absolute zero temperature. Moreover, Crystal Structure Prediction needs to continuously quantify similarities between crystals that can not be distinguished by their chemical compositions. Even for lattices, there was no complete and stable isometry invariant, until two metrics were defined for Voronoi cells [4].

Weighted point-wise distributions [5] and density functions [6] are new stable isometry invariants of any periodic point sets. These invariants have helped us to identify an experimental crystal that was missed in the Cambridge Structural Database, because past comparison tools were unreliable.