For over a hundred years, when confronted by swelling in the brain, surgeons more often than not have resorted to decompressive craniectomy, the traditional route to reducing swelling by removing a large part of the skull. However, while this might be the standard procedure, its failure rate has been worryingly high, primarily because the consequences on the rest of the brain have been poorly understood.
This is no longer just a challenge for neurosurgeons. Mathematicians are now able to study and model the impact of surgery at a cellular level and by so doing develop a more specific picture of the impact of surgery across the whole brain. In particular Oxford Mathematician Alain Goriely and colleagues Johannes Weickenmeier and Ellen Kuhl from Stanford University have looked at the issue by studying a standard physical problem: the problem of bulging in soft solids.
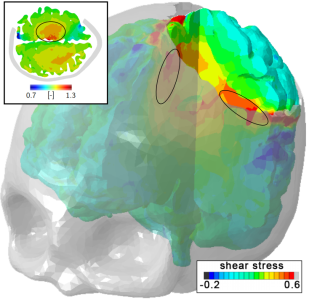
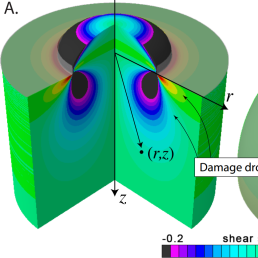
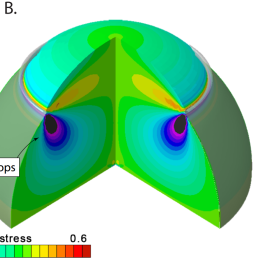
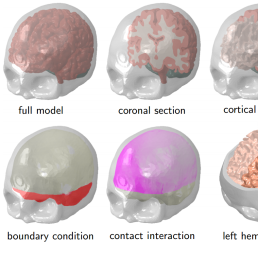
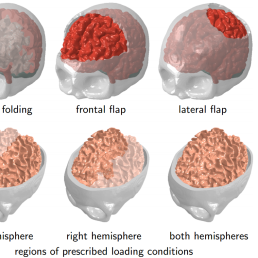
Bulging is due to the swelling of a material while constrained except at an opening, as would be the case when the skull is opened during surgery and the brain bulges out of the skull creating, potentially, deformations in another part of the brain, away from the immediate incision. To quantify possible deformations inside the brain, the team created a personalised finite element craniectomy model from high-resolution medical resonance imaging. Their study reveals three failure mechanisms which would suggest damage beyond the initial incision point: axonal stretch in the centre of the bulge, axonal compression at the edge of the craniectomy, and axonal shear around the opening. Strikingly, even small swelling volumes of 50ml can induce axonal strain in excess of 30% above reported damage thresholds in patients.
Such models suggest a possible mechanism for proving and identifying long-term damage. Indeed, this theoretical study is a first step towards gaining better insight into the complex mechanisms underlying craniectomy and opens the door for systematic personalised studies of craniectomy in patients. The next step is to combine this theoretical work with experimental and clinical work to enable surgeons to provide better-informed and more successful treatments.
A fuller explanation can be found in the following papers:
Journal of the Mechanics and Physics of Solids