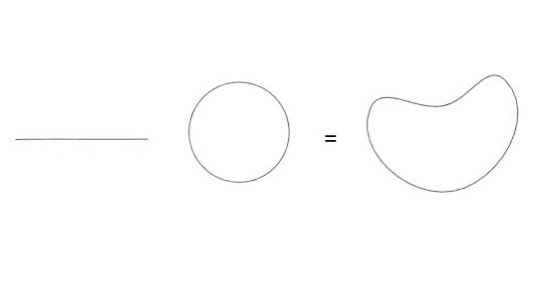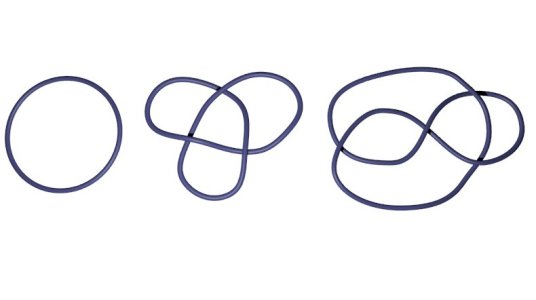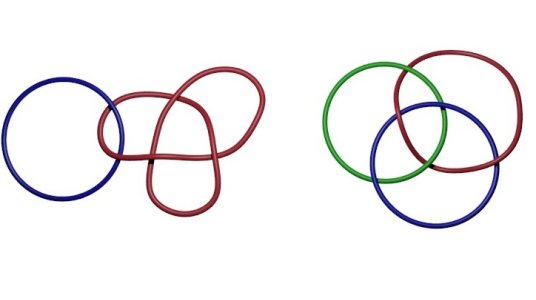Oxford Mathematician Andras Juhasz discusses and illustrates his latest research into knot theory.
"We can only see a small part of Space, even with the help of powerful telescopes. This looks like 3-dimensional coordinate space, but globally it might have a more complicated shape. An n-dimensional manifold, or n-manifold in short, is a space that locally looks like the standard n-dimensional coordinate space, whose points we can describe with n real coordinates. Topology considers such spaces up to continuous or smooth deformations, as if they were made out of rubber.
The only connected 1-manifolds are the real line and the circle. 2-dimensional manifolds are also called surfaces. The closed oriented (or 2-sided) surfaces are the sphere, the surface of a doughnut (the torus), or the surface of a doughnut with several holes. The number of holes is called the genus of the surface, and is an example of a topological invariant: an algebraic object (e.g., a number, polynomial, or vector space) assigned to a space that is unchanged by deformations. We have already seen that we live in a 3-manifold, and, if we add the time dimension, in a 4-dimensional spacetime.
1-manifolds:
2-manifolds (please view all films in Chrome, Firefox or Explorer):
Genus 0 1 2
The theory of 1- and 2-manifolds is classical. Surprisingly, dimensions greater than 4 are simpler than dimensions 3 and 4, due to the fact that there is enough space to perform a certain topological trick that allows one to reduce the classification problem to algebra. The focus of modern topology is hence in dimensions 3 and 4. While 3-manifold topology is closely related to geometry, the theory of smooth 4-manifolds is more analytical. In dimension 4, the difference between smooth and continuous deformations becomes essential. For example, there is just one 4-manifold that looks like 4-dimensional coordinate space up to continuous deformation, but infinitely many of these are smoothly different.
A knot is a circle embedded in 3-space, up to deformation. (Topologically, a knot on a string is always trivial, as one can just pull one end along the string itself until the knot disappears.) A link is a collections of knots that link with each other (hence the name). These play an important role in low-dimensional topology, since every 3- and 4-manifold can be described by a link whose components are each labelled by an integer.
Deformation of an unknot:
Knots:
Links:
Knot Floer homology is an invariant of links defined independently by Ozsváth-Szabó and Rasmussen in 2002. It assigns a finite-dimensional vector space to every link, and contains important geometric information.
Two links are cobordant if they can be connected by a surface in 4-space. If we think of the fourth coordinate as time, each time slice gives a (possibly singular) link. As time varies from say 0 to 1, we obtain a movie of links. In a recent paper published in Advances in Mathematics, I have shown that a link cobordism induces a linear map on knot Floer homology. This can be used to understand the possible surfaces links can bound in 4-space, which is closely related to the topology of smooth 4-manifolds".
A link cobordism: