In a seminal 1952 paper, Alan Turing mathematically demonstrated that two reacting chemicals in a spatially uniform mixture could give rise to patterns due to molecular movement, or diffusion. This is a particularly striking result, as diffusion is considered to be a stabilizing mechanism, driving systems towards uniformity (think of a drop of dye spreading in water). Turing's idea was that this mechanism may underlie how patterning occurs in organisms, as it provides a way for the spontaneous formation of spatial patterns even in systems without any heterogeneity at all. This is reminiscent of Darwin's closing remarks in On the Origin of Species: "[F]rom so simple a beginning endless forms most beautiful and most wonderful[...]''
Since this pioneering work on morphogenesis (how organisms develop), a considerable amount of research has explored the tremendous power of reaction-diffusion models to generate patterns. Despite the success of the theory at capturing the attention of mathematicians, biologists, physicists, and chemists for many decades, there are still things we do not know which are necessary to apply these models to processes in developmental biology. An important example of this, presaged by Turing himself, is that most patterning processes of interest do not emerge from spatial homogeneity, but instead evolve in complex environments, and especially from previous patterns. To quote Turing, "Most of an organism, most of the time is developing from one pattern into another, rather than from homogeneity into a pattern."
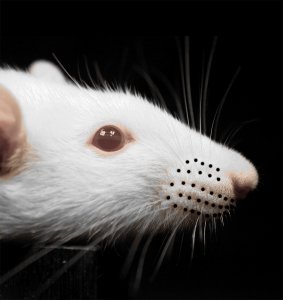
Recently, researchers Andrew Krause and Eamonn Gaffney from Oxford Mathematics together with colleagues from the University of Cardiff, and the Czech Technical University in Prague have been considering Turing's theory to try and explain certain aspects of the patterning of whiskers on mice. They ran simulations of a reaction-diffusion system known to generate spot patterns, but varied some of the model parameters in space, in order to capture some of the observed variation in mice whiskers (in terms of their size and spacing). The figure above shows an example of these spots with variation in space from this model, as well as an example of the arrangement of whiskers in a typical mouse. This work is still in progress, but it has already led to several fundamental insights into these kinds of systems.
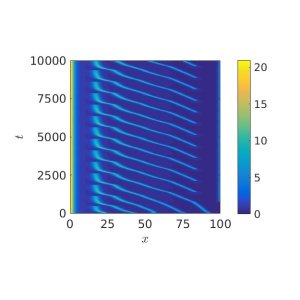
In particular, the researchers found novel patterns which occur in space and time that can be attributed purely to spatial heterogeneity, rather than things which mathematicians are more familiar with that lead to oscillations. Moreover, these oscillating patterns appear robustly in a wide range of different kinds of chemical systems, leading the researchers to think they might be ubiquitous in reaction-diffusion systems. An example of these spatiotemporal oscillations is in the other figure above, where spikes in one spatial dimension are created, move across the spatial domain, and are destroyed, with this pattern repeating periodically in time. The way in which the oscillation period changes as parameters are varied depends crucially on the entire complicated state of the system, contrary to many important models in thermodynamics which display 'universality'.
The researchers hypothesized that it is the interaction of nonlinear reaction and diffusion in a spatially varying medium with an 'open' system that allows for this behaviour. It also calls into question much of the work that has been done using homogeneous models - as Turing himself has said, we anticipate real chemical systems to be in complicated spatial environments. Importantly, very small gradients can lead to moving patterns. Does this occur biologically? Well there are animals who change patterns over time e.g. tapir (slowly changing in time) and flamboyant cuttlefish (rapidly changing in time), but most organisms with spots or stripes, such as zebras or tigers, do not present any kind of oscillations in their coats after birth. The recent work asks many more questions than it answers, both biologically and mathematically. While Turing's original ideas are over 60 years old, he knew that many of his ideas would keep scientists and mathematicians busy for a long time to come, saying "We can only see a short distance ahead, but we can see plenty there that needs to be done.'' The findings appear in the journal Physical Review E.
Figures in rotation:
Reaction-Diffusion model in two spatial dimensions which predicts varying sizes and wavelength between spots.
Typical mouse whisker arrangement (Source: Arrangement of whiskers on the rat's face. Credit: Yan S. W. Yu, Matthew M. Graff, Chris S. Bresee, Yan B. Man, Mitra J. Z. Hartmann (2016) Whiskers aid anemotaxis in rats, Science Advances.)
The chemical concentration over time and space.