Oxford Mathematicians Álvaro Cartea and Leandro Sánchez-Betancourt talk about their work on employing stochastic optimal control techniques to mitigate the effects of the time delay when receiving information in the marketplace and the time delay when sending instructions to buy or sell financial instruments on electronic exchanges.
"In order driven exchanges, liquidity takers face a moving target problem as a consequence of their latency – the time taken to send an order to the exchange. If an order is sent aiming at a price and quantity observed in the limit order book (LOB) then by the time their order is processed by the exchange prices could have worsened, so the order may not be filled; or prices could have improved, so the order is filled at a better price.
Traders can mitigate the adverse effects of missing a trade by including a price limit in their orders to increase the probability of filling the order when it is processed by the Exchange. This price limit consists of the best price seen by the trader in the LOB plus a degree of discretion that specifies the number of ticks the order can walk the LOB and still be acceptable. In other words, for a buy order, the number of ticks included in the discretion specifies the maximum price the trader is willing to pay to fill the order. Similarly, for a sell order, the number of ticks included in the discretion specifies the minimum price the trader is willing to receive to fill the order. This discretion does not preclude the order from being filled at better prices if the LOB is updated with more favourable prices or quantities.
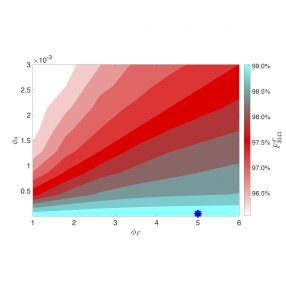
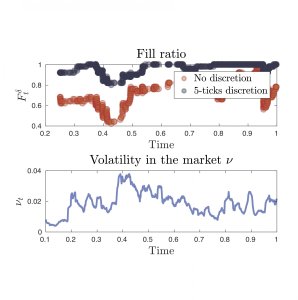
In our paper we show how to choose the discretion of orders in an optimal way to improve fill ratios over a period (days, weeks, months), while keeping orders exposed to receiving price improvement. Increasing fill ratios is costly. Everything else being equal, the chances of filling an order increase if the order can walk the LOB. Thus, there is a tradeoff between ensuring high fill ratios and the execution costs borne by the trading strategy. In our approach, the dynamic optimisation problem solved by the trader balances this tradeoff by minimising the discretion specified in the marketable orders, while targeting a fill ratio over a trading horizon. The trader's optimal strategy specifies the discretion for each transaction depending on the proportion of orders that have been filled, how far the strategy is from the target fill ratio, the cost of walking the LOB, and the volatility of the exchange rate.
We employ a data set of foreign exchange trades to analyse the performance of the optimal strategy developed here. The data are provided by LMAX Exchange (www.lmax.com). We use anonymised transaction data for two foreign exchange traders to compare the fill ratios they achieved in practice to those attainable with the optimal strategy derived in the paper. The data spans a set of dates from December 2016 to March 2017. During this period both traders filled between approximately 80% and 90% of their liquidity taking orders in the currency pair USD/JPY.
We find that the effect of latency on trade fills is exacerbated during times of heightened volatility in the pair USD/JPY. When volatility is arranged in quartiles, we find that between 36% and 40% of unfilled trades occur in the top quartile of volatility.
We employ the optimal strategy developed in our paper to show the tradeoff between increasing fill ratios through the use of discretion and the costs incurred by the strategy. We show that traders could have increased the percentage of filled trades, during the period 5 December 2016 to 30 March 2017, to 99% for both traders. In this example, the average cost incurred by the traders to fill trades missed by the naïve strategy was between 1.24 and 1.76 ticks. On the other hand, the cost of returning to the market 20ms and 100 ms later to fill trades missed by the naïve strategy is between 2.01 and 2.75 ticks respectively.
The performance of the optimal strategy is more remarkable during times of heightened volatility of the exchange rate. In the top quartile of volatility, the average cost of filling missed trades using the optimal strategy is approximately 1.87 ticks, while the mark-to-market average cost of filling the missed trades employing market orders that walk the LOB until filled 100ms later is between 3 and 3.3 ticks.
Finally, we build a function that maps various levels of latency to the corresponding percentage of filled orders. We use this mapping to calculate the shadow price of latency that a particular trader would be willing to pay to reduce the latency of his connection to an exchange. We show that the trader would be better off employing the latency-optimal strategy developed in our paper, instead of investing in hardware and co-location services to reduce latency. The latency-optimal strategy is superior because it not only achieves the same fill ratios as those obtained with better hardware and co-location, but it scoops price improvements that stem from orders arriving with latency at the Exchange."
The full paper may be downloaded here.