Over the last few years, the study of the physiological mechanisms governing the movement of fluids in the brain (referred to as the brain waterscape) has gained prominence. The reason? Anomalies in the brain fluid dynamics are related to diseases such as Alzheimer's disease, other forms of dementia and hydrocephalus. Understanding how the brain waterscape works can help discover how these diseases develop. Unfortunately, experimenting with the human brain in vivo is extremely difficult and the subject is still poorly understood. As a result, this topic is a highly active interdisciplinary research area. In our research team, formed by Oxford Mathematicians Matteo Croci, Patrick Farrell and Mike Giles in collaboration with Marie E. Rognes, Vegard Vinje and colleagues from Simula Research Laboratory, we contribute by simulating the brain waterscape on a computer, hence providing an alternative avenue of investigation that is cheap and does not require human experimentation.
One of the main challenges in brain simulation is the lack of accurate quantitative information on the mechanical input parameters needed to set up our mathematical model. Quantities such as brain matter permeability, interstitial fluid flow velocity and diffusivity are only known approximately or on average. The position of the blood vessels and capillaries can be measured, but it varies from patient to patient and it is extremely difficult to resolve without significant expense.
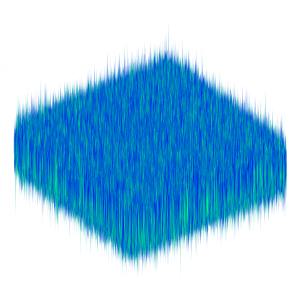
To overcome these issues, we can construct surrogates for these quantities that account for the uncertainty in their values through the use of Gaussian random fields. Gaussian random fields are functions of space whose values at each point are given by Gaussian random variables which are correlated according to a given covariance function. Sampling realisations of these fields can be extremely expensive computationally. Our team of researchers developed one of the fastest currently available sampling algorithms for Mat\'ern-Gaussian fields. This is achieved by recasting the Gaussian field sampling problem as the solution of an elliptic partial differential equation (PDE) driven by spatial white noise. Solving this equation is standard, but sampling white noise is not. The developed algorithm is able to draw white noise realisations quickly and efficiently and can be used in conjunction with the multilevel Monte Carlo (MLMC) method for further acceleration (see here). The coupling of white noise required by MLMC is enforced even in the non-nested case thanks to a supermesh construction. Furthermore, the algorithm can be employed to solve a wider class of PDE problems with spatial white noise additive terms.
For further information on the efficient sampling and coupling of white noise for MLMC with non-nested meshes see here. A paper on uncertainty quantification in brain simulation is in preparation and a link will appear here in due course.