If you type fundamental anagram of calculus into Google you will be led eventually to the string of symbols 6accdæ13eff7i3l9n4o4qrr4s8t12ux, probably accompanied by an explanation more or less as follows: this is a recipe for an anagram - take six copies of a, two of c, one of d, one of æ and so on, then rearrange these letters into a chunk of Latin. The accepted solution is Data æquatione quotcunque fluentes quantitates involvente fluxiones invenire et vice versa although this has nine copies of t rather than eight, and this lack of a t is assumed to be an error of the author, who was Isaac Newton and who recorded the solution in a notebook. The string occurs in a letter of Newton from 1676, sent to the mathematician Leibniz via Henry Oldenburg, who was the first Secretary of the Royal Society and a much-used conduit for savants. Newton was seeking to establish priority in the invention of calculus without giving anything away. The string is preceded in Newton's letter by the sentence "...[B]ecause I cannot proceed with the explanation of it now, I have preferred to conceal it thus:". In other words he meant to hide his knowledge but still establish priority. Online translations give the meaning of the Latin as Given an equation involving any number of fluent quantities to find the fluxions, and vice versa, which would suggest it is disguising the fundamental theorem of calculus, 'fluents' and 'fluxions' being Newton's terms for time-varying quantities and their derivatives, but one can find looser translations online, along the lines of Differential equations rock or rule or are the way to go, and I'm voting for one of those here.
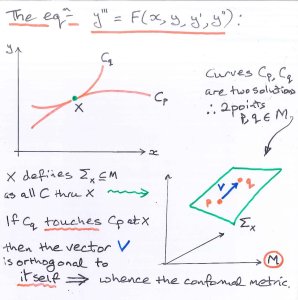
Newton was a great geometer and phrased his Principia Mathematica in the language of geometry, when a greater use of differential equations might have made it more accessible. Newton would probably have been pleased (if he was ever pleased) to see geometry re-emerging from the study of differential equations and that is what I want to describe here. Given an ordinary differential equation of some order, say $N$, and written as \begin{equation}\label{1} \frac{d^Ny}{dx^N}=F\left(x,y,\frac{dy}{dx},\ldots,\frac{d^{N-1}y}{dx^{N-1}}\right), \;\;\;\;\;\;\;\;\;(1)\end{equation} one can contemplate the set of all possible solutions. Call this $M$ (for moduli space, a common usage) then $M$ has $N$ dimensions, as one sees as follows: choose a value of $x$, say zero for simplicity, and specify the $N$ numbers $\left(y(0),dy/dx|_0,\ldots,d^{N-1}y/dx^{N-1}|_0\right)$, where the notation '$|_0$' should be read as 'evaluated at $x=0$', then, subject to reasonable conditions on $F$, there is one and only one solution of (1) with these values. Thus a point of $M$ is specified by $N$ numbers, which is what you mean by '$M$ having $N$ dimensions'.
If the function $F$ is linear, that is of the form \[F(x,y_0,y_1,\ldots,y_{N-1})=\alpha_0(x)y_0+\alpha_1(x)y_1+\ldots+\alpha_{N-1}(x)y_{N-1}\] then $M$ is a vector space and, for our purposes, flat and dull; but if $F$ is nonlinear then $M$ can be quite interesting.
I'll illustrate this with an example that goes back to the French mathematician Elie Cartan in 1943, [1], but which had a new lease of life from the 1980s, (see e.g. [2], [3]). Take $N=3$, so we are interested in nonlinear, third-order differential equations with corresponding three-dimensional moduli space $M$ of solutions. One thinks of $M$ as a manifold, imagine something like a smooth surface in some higher-dimensional Euclidean space, on which one can move around smoothly. Can one give $M$ a conformal metric? This is a rule for measuring angles between directions at any point, and is a slightly weaker notion than measuring lengths of vectors at any point (an angle being essentially obtained from a ratio of lengths), and it turns out that one can provided $F$ satisfies a certain condition. The condition is a bit messy to write down, so I won't, but really it has to be because it must still hold if we make new choices of $x$ and $y$ according to the change \[(x,y)\rightarrow(\hat{x},\hat{y})=(f(x,y),g(x,y)),\] for any $f$ or $g$, which certainly makes a big change in $F$, but not much change in M (for the expert: there is more freedom than this, of contact transformations rather than just point transformations).
Now one asks another question: can one also give $M$ a conformal connection (which can be thought of as a way of moving angles around and comparing them at different places)? Again there is a single condition on $F$ that allows this, and the upshot, noticed by Cartan, is that given these two conditions on $F$, the moduli space $M$ of solutions of $F$, with its conformal metric and connection, automatically satisfies the most natural conditions in three-dimensions which generalise the Einstein equations of general relativity in four-dimensions. This is really like a-rabbit-out-of-a-hat, and is typical of what happens in this study of the geometry of differential equations.
My second example is more complicated to describe - things get harder quickly now. Here we're following [4] but slightly rephrased as in [5], [6]. Consider then the following quite specific fifth-order differential equation: \begin{equation}\label{2} \left(\frac{d^2y}{dx^2}\right)^{\!2}\frac{d^5y}{dx^5}+\frac{40}{9}\left(\frac{d^3y}{dx^3}\right)^{\!3}-5\frac{d^2y}{dx^2}\frac{d^3y}{dx^3}\frac{d^4y}{dx^4}=0.\;\;\;\;\;\;\;\;(2) \end{equation} Of course this can be rearranged to look like (1) but I've written it like this to avoid denominators. It isn't too hard to solve (2), especially if you notice first that it is equivalent to \[\frac{d^3}{dx^3}\left[\left(\frac{d^2y}{dx^2}\right)^{\!-2/3}\right]=0.\] One rapidly finds that the general solution can be written implicitly as \begin{equation}\label{3}(\begin{array}{ccc} x & y & 1\\ \end{array})\left(\begin{array}{ccc} a_1&a_2&a_3\\ a_2&a_4&a_5\\ a_3&a_5&a_6\\ \end{array}\right)\left(\begin{array}{c}x\\ y\\ 1\\ \end{array}\right)=0, \;\;\;\;\;\;\;\;(3)\end{equation} where $a_1,\ldots,a_6$ are constants (there are six of these and we expect the solution to depend on only five constants, but there is freedom to rescale all six by yet another constant, which reduces the six to an effective five). For convenience we'll allow all quantities $x,y,a_1,\ldots,a_6$ to be complex now, and then (3) can be interpreted as a conic in the complex projective space ${\mathbb{CP}}^2$ (this is like a familiar conic in two-dimensions but complexified and with points added 'at infinity'). Thus $M$, the moduli space of solutions of the fifth-order differential equation (2) can be regarded as the five-complex-dimensional space of such conics. This $M$ is a symmetric space and as such has a metric satisfying the Einstein equations in this dimension. We can say a bit more about this metric: a vector at a point $p\in M$ can be thought of as two infinitesimally-separated conics (one at each end of the vector, thinking of the vector as a tiny arrow), and two conics meet in four points (at least in the complex and with points at infinity included). Thus a vector tangent to $M$ factorises into a product of four two-component 'vectors' (which are in fact spinors). In an index notation a vector $V$ can be written in terms of its components as \[V^a=V^{ABCD}=\alpha^{(A}\beta^B\gamma^C\delta^{D)},\] where $a$ runs from 0 to 4, $A,B,C,\ldots$ from 0 to 1, $\alpha,\beta,\gamma,\delta$ correspond to the four intersections of the infinitesimally-separated conics, and the round brackets imply symmetrisation of the indices contained. In a corresponding way the metric or Levi-Civita covariant derivative factorises: \[\nabla_a=\nabla_{ABCD}.\]Consequently the (linear, second-order) differential equation \begin{equation}\label{4}\nabla_{PQ(AB}\nabla_{CD)}^{\;\;\;\;PQ}\Phi=\lambda\nabla_{ABCD}\Phi,\;\;\;\;\;\;\;\;(4)\end{equation} for a scalar function $\Phi$ on $M$ and a constant $\lambda$ makes sense (the spinor indices are raised or lowered with the spinor 'metric' $\epsilon_{AB}$ or $\epsilon^{AB}$ from which the metric of $M$ can be constructed).
Now here comes the rabbit out of the hat: one fixes a specific $\lambda$ and chooses a solution $\Phi$ of (4) with a non-degeneracy property \begin{equation}\label{5}\Phi_{ABCD}\Phi^{AB}_{\;\;\;PQ}\Phi^{CDPQ}\neq0\mbox{ on }\Phi=0,\;\;\;\;\;\;\;\;(5)\end{equation} (and here $\Phi_{ABCD}=\nabla_{ABCD}\Phi$); we are going to define a new metric on the four-dimensional surface $N=\{\Phi=0\}\subset M$ and we accomplish this by choosing two linearly independent solutions $h_{(1)}^{ABC},h_{(2)}^{ABC}$ of \[\Phi_{ABCD}h_{(i)}^{BCD}=0\mbox{ on }\Phi=0,\] an equation which has a two-dimensional vector space of solutions by virtue of the nondegeneracy condition (5) that we've imposed; then one carefully chooses a linearly independent pair of spinors (or spinor dyad) $(o^A,\iota^A)$ for $M$ and constructs the set of four linearly-independent vectors (or tetrad) \[e_1=o^{(A}h_{(1)}^{BCD)},\;e_2=\iota^{(A}h_{(1)}^{BCD)},\;e_3=o^{(A}h_{(2)}^{BCD)},\;e_4=\iota^{(A}h_{(2)}^{BCD)};\] this is a tetrad of vectors tangent to $N$ and determines a metric on $N$ by \[g=e_1\odot e_4-e_2\odot e_3.\] The rabbit is that this metric automatically has special curvature, in fact it has anti-self-dual Weyl curvature, and a bit more besides: see [5] for details.
For more on Paul's work click here.
[1] E. Cartan, Sur une classe d'espaces de Weyl, Annales scientifiques de l'E.N.S. 3e série, tome 60 (1943), 1-16
[2] N.J.Hitchin, Complex manifolds and Einstein's equations. Twistor geometry and nonlinear systems (Primorsko, 1980), 73-99, Lecture Notes in Math., 970, Springer, Berlin-New York, 1982.
[3] P.Tod, Einstein-Weyl spaces and third-order differential equations. J. Math. Phys. 41 (2000) 5572-5581.
[4] D Moraru, A new construction of anti-self-dual four-manifolds. Ann. Glob. Anal. Geom. 38, (2010), 77-92.
[5] M. Dunajski and P. Tod, Conics, Twistors, and anti-self-dual tri-Kahler metrics
[6] M. Dunajski and P. Tod, An example of the geometry of a 5th-order ODE: the metric on the space of conics