The problem of optimisation – that is, finding the maximum or minimum of an ‘objective’ function – is one of the most important problems in computational mathematics. Optimisation problems are ubiquitous: traders might optimise their portfolio to maximise (expected) revenue, engineers may optimise the design of a product to maximise efficiency, data scientists minimise the prediction error of machine learning models, and scientists may want to estimate parameters using experimental data. In real-world settings, uncertainties and errors are unavoidable, and this can cause stochastic noise to be present in the objective.
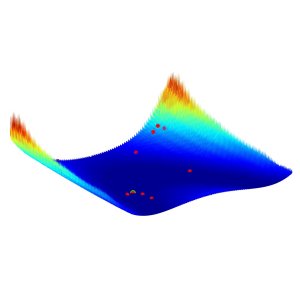
Most methods for optimisation rely on being able to evaluate both the objective and its derivatives. Access to first derivatives is important for finding uphill or downhill directions, which tell us where to search next for optima, and when to terminate the method. However, when the objective has stochastic noise, it is no longer differentiable, and standard optimisation methods do not work. Instead, we must develop ‘derivative-free’ optimisation methods; that is, we have to answer the question “how do you get to the top of a hill when you don’t know which way is up?”. We achieve this by constructing models of the landscape based on sampling objective values – this approach is based on rigorous mathematical principles, and has provable guarantees of success. The figure above shows a noisy landscape, and the points tested by a derivative-free method searching for the true minimum (bottom centre, in green).
Oxford Mathematicians Lindon Roberts and Coralia Cartis, together with Jan Fiala and Benjamin Marteau from Numerical Algorithms Group Ltd (NAG), a British scientific computing company, have developed a new derivative-free method for optimising noisy and expensive objectives. The method automatically detects when the information in the objective value is overwhelmed by noise, and kick-starts the method to bring more information into the models of the landscape. This approach requires fewer evaluations of the (possibly expensive) objective, runs faster and is more scalable, but produces as good solutions as other state-of-the-art methods. Their ideas are being commercialised by NAG and will soon be available in their widely-used software library. This technique is also being applied to parameter estimation for noisy climate simulations, to help scientists find optimal parameters that fit observational climate data, thus helping quantify the sensitivity of our climate to CO2 emissions.
This work is supported by the EPSRC Centre for Doctoral Training in Industrially-Focused Mathematical Modelling.