Oxford Mathematician Tsou Sheung Tsun talks about her work on building the Framed Standard Model and the exciting directions it has taken her.
"I have been working, in collaboration with José Bordes (Valencia) and Chan Hong-Mo (Rutherford-Appleton Laboratory), to build the Framed Standard Model (FSM) for some time now. The initial aim of the FSM is to give geometric meaning to (fermion) generations and the Higgs field(s). The surprise is that doing so has enabled one not only to reproduce some details of the standard model with fewer parameters but also to make testable new predictions, possibly even for dark matter. I find this really quite exciting.
It is well known that general relativity is solidly based on geometry. It would be nice if one can say the same for particle physics. The first steps are hopeful, since gauge theory has geometric significance as a fibre bundle over spacetime, and the gauge bosons are components of its connection.
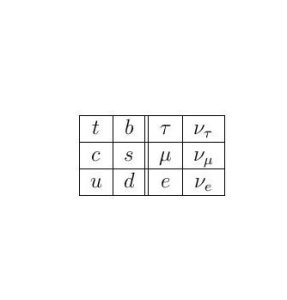
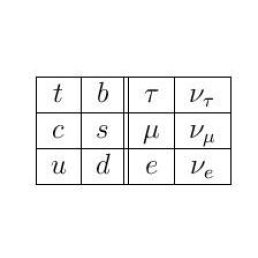
The standard model (SM) of particle physics is a gauge theory based on the gauge group $SU(3) \times SU(2) \times U(1)$, ignoring discrete identifications for simplicity. The gauge bosons are the photon $\gamma$, $W^\pm, Z$ and the colour gluons. To these are added, however, the scalar Higgs fields, and the leptons and quarks, for which no geometric significance is usually sought nor given. Besides, the latter two have to come in three generations, as represented by the three rows of the table below.
In a gauge theory the field variables transform under the gauge group. and to describe their transformation, we need to specify a local (spacetime dependent) frame, with reference to a global (fixed) frame via a transformation matrix. We suggest therefore that it is natural to incorporate both the local and global symmetries, and to introduce the elements of the transformation matrix as dynamical variables, which we call framons. Consequently, the global $SU(3)$ symmetry can play the role of generations, and the $SU(2)$ framons can give rise to the Higgs field.
The FSM takes the basic structure of the SM, without supersymmetry, in four spacetime dimensions, adds to it a naturally occuring global symmetry, and uses 't Hooft's confinement picture instead of the usual symmetry breaking picture.
As a result of this suggestion, we find that many details of the SM can be explained. Indeed, already by one-loop renormalization, we are able to reproduce the masses of the quarks and leptons, and their mixing parameters including the neutrino oscillation angles, using 7 parameters, as compared to the 17 free parameters of the SM. It also gives an explanation of the strong CP problem without postulating the existence of axions.
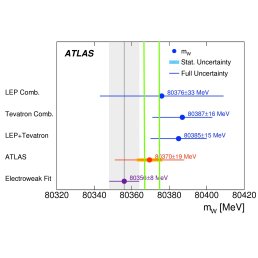
In addition, the FSM has predictions which are testable in the near future. What is special about the FSM is the presence of the colour $SU(3)$ framons. They will have effects which make the FSM deviate from the SM. Let me mention one of these which is of immediate relevance to LHC experiments. The FSM has a slightly larger prediction for the mass of the $W$ boson than the SM (see figure). It would be very interesting to see if future improved measurements of the $W$ mass would agree better with FSM.
(Figure 1: Measurements of the W boson mass compared to the SM prediction (mauve) and the FSM predictions (green) at two different vaccuum expectation values).
One other possible implication is that some of the bound states involving the $SU(3)$ framons might be suitable candidates for dark matter. Now dark matter is one of the astrophysical mysteries still largely unresolved. We know that constituents of dark matter, whatever they may be, have mass but hardly interact with our world of quarks and leptons. These FSM candidates have exactly these properties, but we need more study to see if they are valid candidates for dark matter. If they were, then it would be a very interesting implication for the FSM."
For a fuller explanation of the work click here.