Executive stock options (ESOs) are contracts awarded to employees of companies, which confer the right to reap the profit from buying the company stock (exercising the ESO) at or before a fixed maturity time $T$, for a fixed price specified in the contract (the strike price of the ESO). ESOs are used to augment the remuneration package of employees, the idea being to give them an incentive to boost the company's fortunes, and thus the stock price, making their ESO more valuable.
It has been argued that holders of ESOs could exploit their inside information on the company to advantageously exercise in advance of upcoming bad news that would cause the stock price to fall, news which is yet to be publicly revealed. Empirical studies of ESO exercise have indicated that such options tend to be exercised prior to poor stock performance. The question is whether this is due to some informational advantage.
There have been few if any mathematical models which have been able to capture such potential information effects. Oxford Mathematicians Michael Monoyios and Christoph Reisinger and co-authors have constructed models which incorporate privileged information on the evolution of a stock price, to analyse and illustrate exercise patterns in the presence of inside information.
One such model (1) features a stock whose expected return (or drift) parameter suffers a change point at an exponentially distributed random time $\theta$, independent of the Brownian motion driving the stock; its drift falls from its initial constant value $\mu_{0}$ to a lower constant value $\mu_{1}<\mu_{0}$.
In this scenario we studied two optimal stopping problems, to find the best exercise time for agents with different information on the change point. The two problems are distinguished by full information, in which the change point as well as the stock price is observed, or by partial information, in which the change point is not observable, and so is filtered (or estimated) from observations of the stock price. The fully informed agent is to be thought of as a senior executive, privy to upcoming bad news (think of the VW emissions scandal), while the partially informed agent is a less senior employee.
The information differential leads to the two agents having different perceptions of the stock price drift, so they perceive different dynamics for the stock price. Mathematically, the different information flows are modelled by filtrations: sets of events (increasing in size as time flows) which can be determined
to have happened (or not) by each agent. The stock drift for the fully informed agent is $\mu(Y)$, given by
\begin{equation*}
\mu(Y_{t}) := \mu_{0}(1-Y_{t}) + \mu_{1}Y_{t} = \left\{\begin{array}{ccc}
\mu_{0}, & \mbox{on} & \{t<\theta\}=\{Y_{t}=0\}, \\
\mu_{1}, & \mbox{on} & \{t\geq\theta\}=\{Y_{t}=1\},
\end{array}\right. \quad t\in[0,T],
\end{equation*}
where
\begin{equation*}
Y_{t} := \left\{\begin{array}{ccc}
0, & \mbox{on} & \{t<\theta\}, \\
1, & \mbox{on} & \{t\geq\theta\},
\end{array}\right. , \quad t\in[0,T],
\end{equation*}
is the indicator process that the change point has occurred. On the other hand, the drift seen by the partially informed agent is a diffusion process given by
\begin{equation*}
\mu(\widehat{Y}_{t}) := \mu_{0}(1-\widehat{Y}_{t}) +
\mu_{1}\widehat{Y}_{t}, \quad t\in[0,T],
\end{equation*}
with $\widehat{Y}$ a diffusion in $[0,1]$ representing the partially informed agent's best estimate of the process $Y$.
We analysed the optimal exercise problems for each agent in these models, both featuring random drift processes (and this is where the mathematical and numerical challenge lies), to examine how the different information could lead to advantageous exercise for the fully informed agent.
The fully informed agent's strategy is characterised by two exercise thresholds, a pair of ordered, non-increasing, time-dependent exercise boundaries $x^{*}_{0}(t)\geq x^{*}_{1}(t),\,t\in[0,T]$, such that optimal early exercise occurs in the state where the drift is $\mu_{i},i\in\{0,1\}$, as soon as the stock breaches $x^{*}_{i}(\cdot)$ from below, or if such a breach is triggered by the change point.
On the other hand, the partial information exercise boundary is a surface $x^{*}(t,y),\,t\in[0,T],\,y\in[0,1]$, with an additional spatial dependence on a variable $y\in[0,1]$, arising from the dependence of the drift on the filtered change point process $\widehat{Y}$, and such that the partial information exercise surface lies between the full information exercise thresholds.
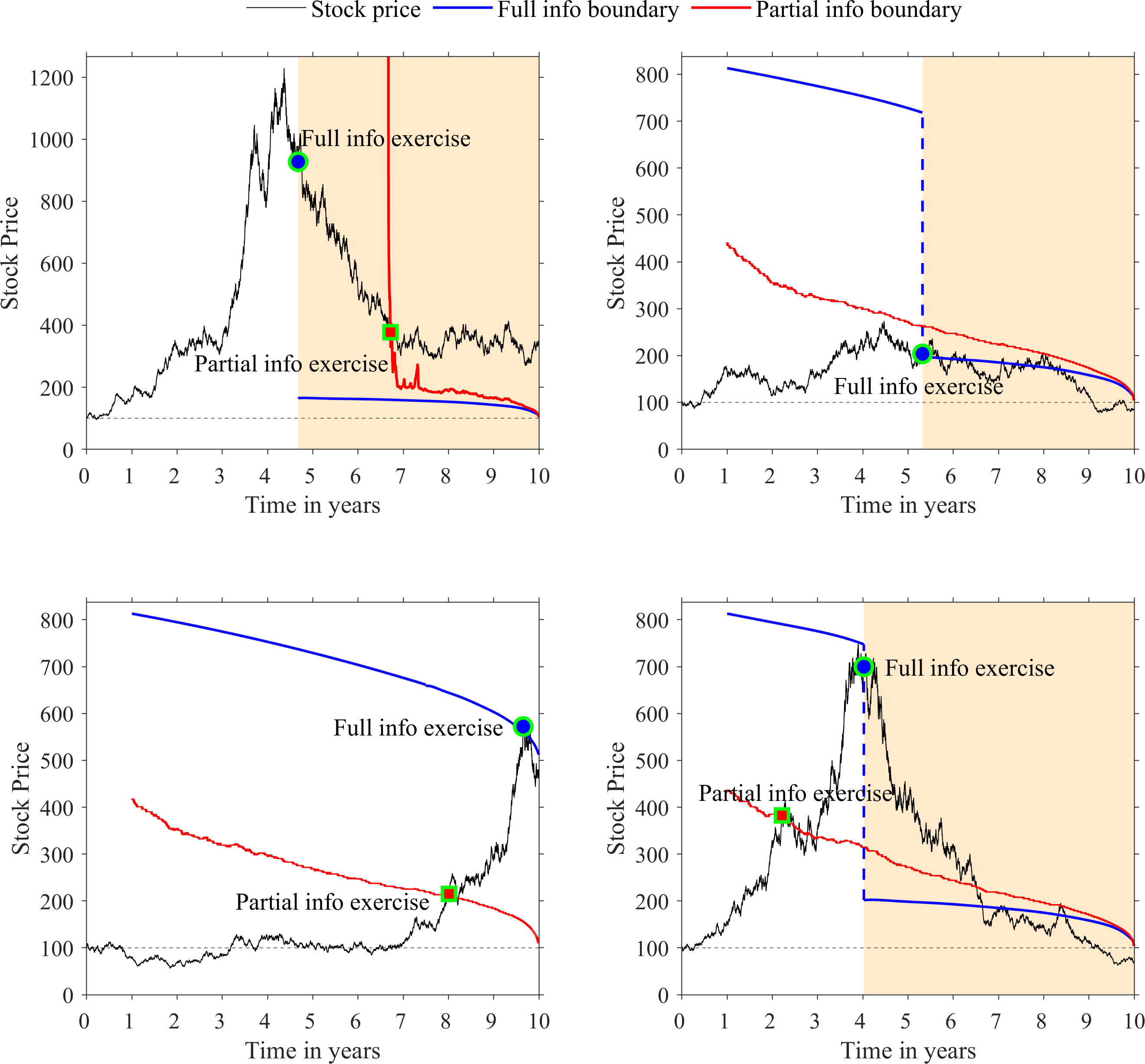
We showed that this can lead to an interesting range of possible exercise patterns, such as immediate exercise by the fully informed agent in response to the change point, a strategy unavailable to the agent who does not see the jump in drift. In this vein, the figure below shows some simulations which illustrate the possible exercise patterns, indicating how complete information on the change point leads to a greater exercise profit.
Image above: simulations of stock price path, full information exercise boundaries (blue) and a cross-section of the partial information exercise boundary (red). Exercises of the fully informed agent are marked with circles, with those of the partially informed agent marked by squares. In each panel, the shaded background indicates the switch in drift regime to $\mu_1 < \mu_0$.
An earlier model for ESO exercise with inside information was constructed by Monoyios and DPhil student Andrew Ng (2). Here, the inside information was modelled by assuming the agent had advance information on the value of the stock at the ESO maturity time. Mathematically, one uses techniques known as enlargement of filtration to compute the dynamics of the stock price as seen by the insider. Once again, the informational advantage was evident in the exercise strategy.
Full details of these models appear in the two papers below:
[1] V. Henderson, K. Kladıvko, M. Monoyios, and C. Reisinger, Executive stock option exercise with full and partial information on a drift change point. arXiv preprint 1709.10141, 2020.
[2] M. Monoyios and A. Ng, Optimal exercise of an executive stock option by an insider, Int. J. Theor. Appl. Finance, 14 (2011), pp. 83–106