How do we design face masks that efficiently remove contaminants while ensuring that we can still breathe easily? One complicating factor with this question is the fact that the properties of the material that we start off with for our face mask can be very different when in use. A key example is seen when you stretch the mask around your face to put it on. In doing so, you also stretch the pores, i.e., the holes in the material that allow the air to pass through. This means that some contaminants that would ordinarily have been trapped by the mask can now pass through the material. Another example is the fact that, when you inhale, the material will compress due to the suction force you apply. This process has the opposite effect, with the pores shrinking. While pore shrinkage is desirable for efficient trapping of contaminants it also makes it more difficult to breathe through the mask. Crucially, in both these cases, when the filter is being used it may work less well than expected.
Oxford Mathematicians Ian Griffiths, Colin Please, Jakub Köry & Armin Krupp have tackled this problem by studying how pressure differences in the air, such as those arising due to inhalation, change the properties of a filter material. They use classical models of linear elasticity for deformation of the filter material and Darcy flow for movement of the air, and then couple these by accounting for how stresses in the material change the pore size, as described in the examples above, and hence the flow.
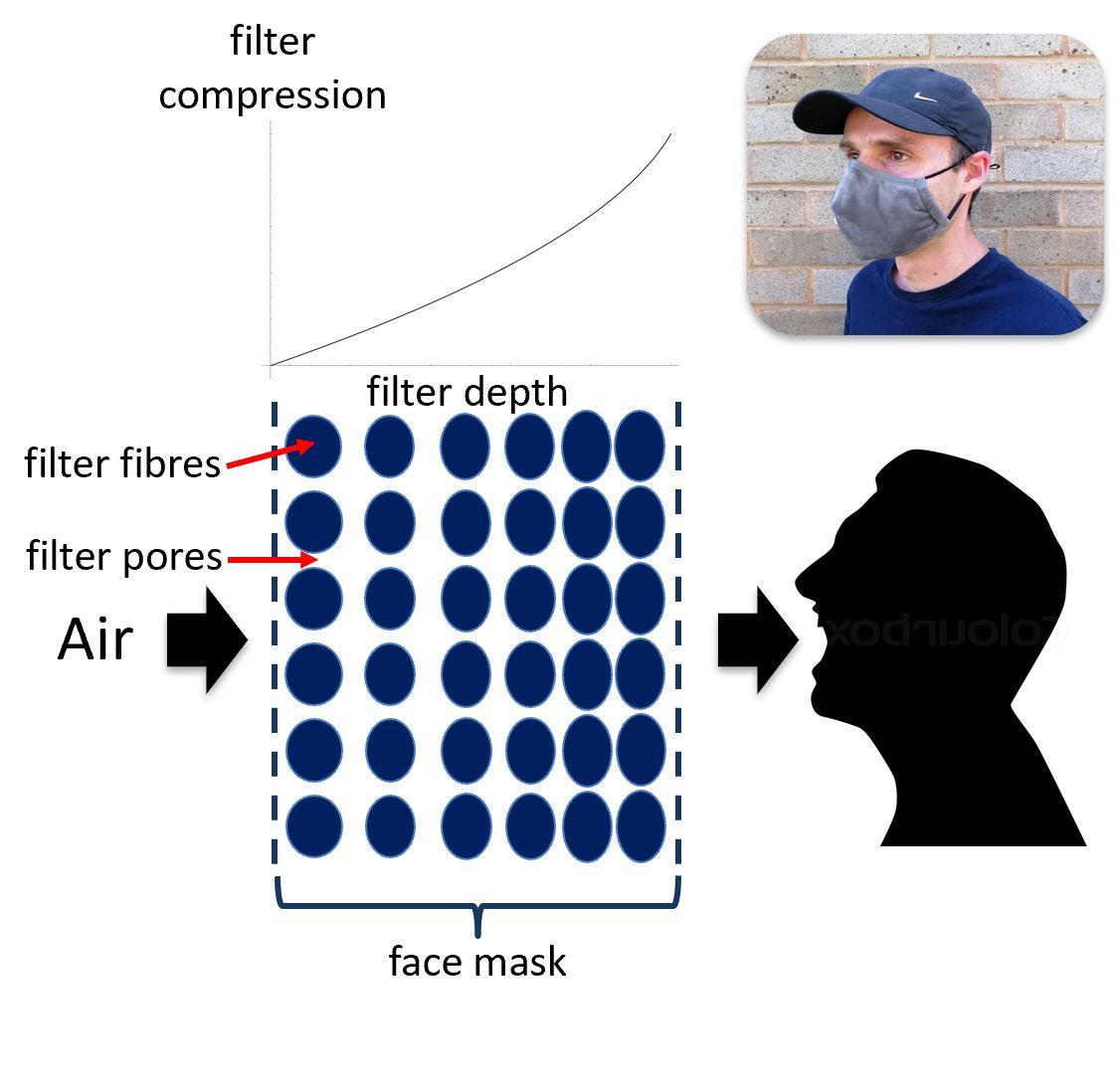
The resulting mathematical model allowed the team to explore and quantify how the filter behaves in operation. The first observation they found was that, upon inhalation, the material does not compress uniformly: the material that is closest to our face compresses the most and the part of the mask that is furthest away from our face and exposed to the air compresses the least (see figure below). This non-uniform material compression means that the filter is not behaving optimally: it is neither removing the contaminants in the desired way nor allowing us to breathe as easily as possible. Furthermore, if we inhale too hard then eventually the material next to our face will be compressed so much that the pores that allow the air to flow through will completely close up. In this case, the material will ‘shut down’ and no air at all can flow.
These observations lead to posing the question of how we could design a filter material that has the properties we desire when in operation. This is a question that has a much broader reach than the example of face masks presented here: every filter that is used, from the household filters that you find in your vacuum to industrial-scale filters that provide clean air in a building, require certain filtration properties when in operation rather than when the device is not in use and the material is in its rest state.
The question of how to design a filter that has particular properties when in use is an inverse problem: we need to design the filter material in its rest state in such a way as to achieve a specified property when in operation. The mathematical model the team have developed allows us to tackle such a problem. Two scenarios are examined. First, the case where we want to design a filter material that has uniform permeability when in operation. This avoids the scenario shown in the figure where compression causes the permeability of the material to be lower the closer we get to our face. A filter with uniform permeability is effective at removing contaminants throughout its depth and also makes it as easy as possible to breathe. Second, the case where we want a filter design that provides the maximum flow rate before shutting down. Such filters are desirable in industrial settings such as ventilation systems, where the key challenge is to maximise the amount of air that is filtered.
This model is now being developed to explain how such filters perform and evolve as they remove contaminants. The resulting models can then be used to answer important questions concerning the design of efficient filters in the future.
Figure: as air passes through the pores between the filter fibres that constitute a face mask, the material compresses. The amount of compression increases the closer we move to the face.