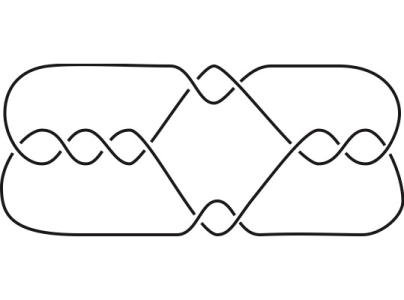
Take a piece of rope and knot it as you wish. When you are done, glue the two extremities together and you will obtain a physical realisation of what mathematicians also call a knot: a simple closed curve in 3-dimensional space. Now, put the knotted rope on a table and take a picture of it from above. It is now a planar projection of your knot. The mathematical equivalent of it is a knot diagram with multiple crossings as shown in the figure. The mathematical challenge is to decide whether a given knot diagram is actually the ‘unknot’, which means that by moving the knot around, you could deform it to a round circle. This question was formulated by Max Dehn in 1910, and was highlighted by Alan Turing in his final published paper:
"No systematic method is yet known by which one can tell whether two knots are the same." - 'Solvable and Unsolvable Problems', Science News 31, pp 7-23 (1954)
An algorithm that determines whether a knot is unknotted was first given by Wolfgang Haken in 1961. There are now many different algorithms that solve this problem, using a wide variety of techniques from low-dimensional topology and geometry. However, most of these algorithms are extremely slow for complicated knots and a famous unresolved question is whether there exists an algorithm that runs in polynomial time, which means that its running time is a polynomial p(n) that depends on the number of crossings n.
‘A lot of people have thought about this question ... but this has been a very hard question to resolve.’ (William Thurston, 2011)
In a remarkable Gordian tour-de-force, Oxford Mathematician Marc Lackenby has created an algorithm that determines whether a knot is the unknot in n^{c log(n)} steps, for some constant c, which is known as quasi-polynomial time. This is only slightly slower than polynomial time, and represents a significant advance over what previously was known. Marc outlined his algorithm in a seminar at University of California, Davis on 2 February and a recording of his talk is available. You can also view his slides for that talk. Marc also spoke to BBC World Service about his work and its wider applications.
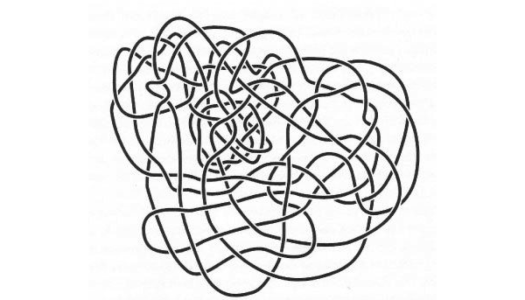
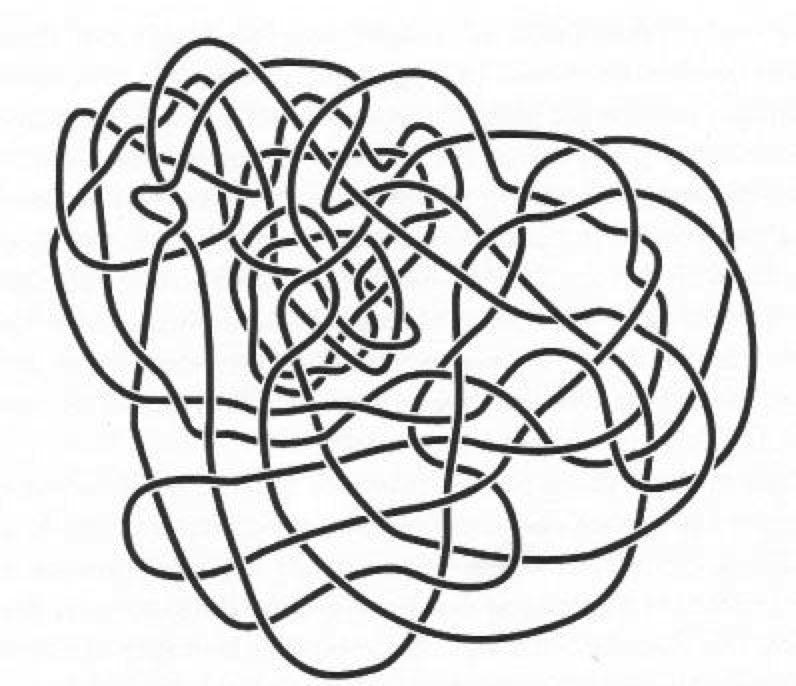
Figure below: two very tangled diagrams that are both actually the unknot.