Oxford Mathematician William Hart and former Oxford Mathematician Dr Robin Thompson (now an Assistant Professor at the University of Warwick) discuss their latest joint COVID-19 research (carried out with fellow Oxford Mathematician Philip Maini), using mathematical models to infer changes in infectiousness during SARS-CoV-2 infections.
"When a person is infected by SARS-CoV-2 [the virus that causes COVID-19], the risk that they go on to infect someone else varies during their course of infection. Changes in the amount of virus within the infected person affect this transmission risk, as do behavioural factors such as the number of contacts that they have with others.
Understanding the effectiveness of public health measures introduced to combat the COVID-19 pandemic requires changes in infectiousness during an infection to be assessed. For example, isolation strategies are only likely to be effective if infected individuals are isolated over the period when they are most infectious. Consequently, there is widespread interest in estimating how infectiousness varies during infection.
Most previous studies estimating changes in infectiousness during a SARS-CoV-2 infection have made an unrealistic assumption: the risk of an individual transmitting the virus does not depend on when exactly during infection they develop symptoms (i.e. whether they are pre-symptomatic or symptomatic at a given time since infection). In fact, infected individuals might in reality be less likely to infect others once they develop symptoms, because they are then more likely to stay at home.
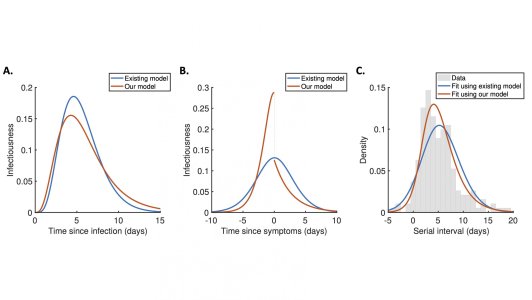
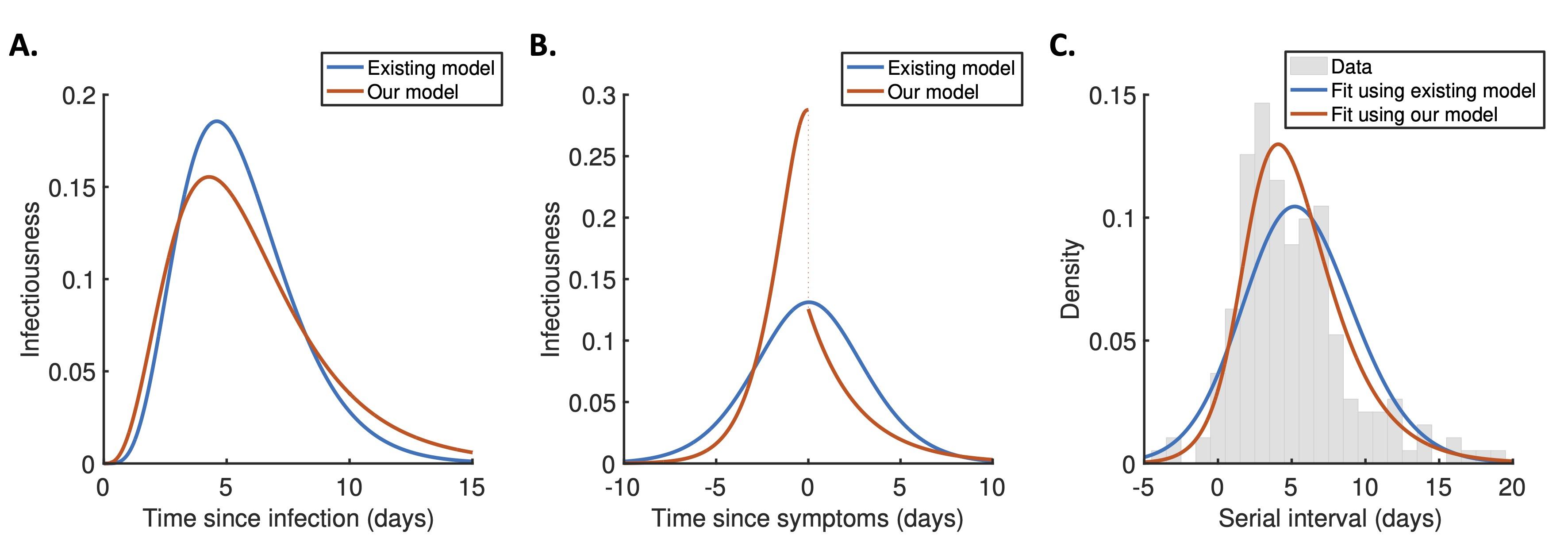
We developed a new framework for estimating how an infected person’s infectiousness changes during a SARS-CoV-2 infection, explicitly linking the transmission risk to when they develop symptoms. Our method provides an improved fit to data from SARS-CoV-2 infected individuals compared to existing approaches. Our model predicts that a high proportion of transmissions (around 65%) occur before symptoms develop. Further, the transmission risk is highest immediately before symptoms. This highlights the importance of identifying people who have come into contact with known infected individuals. If these contacts can be found and isolated before they develop symptoms, then transmission of the virus can be reduced.
Our major finding – that many transmissions occur shortly before symptoms – is of interest to public health policy makers. The new methodology, and our estimates of changes in the transmission risk during infection, are also useful for epidemic modellers working on COVID-19 and other diseases. Our research will help to make other models more accurate, including models used for projecting future numbers of cases or deaths and models used to estimate changes in the R number.
We used data from the early months of the pandemic in our study. Since then, we have been exploring how characteristics of transmission have changed as the pandemic has progressed. While our original article used data from different countries, we recently released a new preprint exploring how transmission has changed in the UK during the pandemic, using household data collected by Public Health England. Models used to inform policy should include the most accurate possible estimates of infectiousness, to ensure that implemented interventions are based upon the best available evidence. This includes using up-to-date estimates, ideally from the specific location under consideration."
Figure caption. A. The expected infectiousness of an infected individual at each time since infection, predicted either using a commonly used approach in which infectiousness is assumed to be independent of when the individual develops symptoms (blue), or using our mechanistic model which explicitly links infectiousness to symptoms (red). B. Equivalent to panel A but instead showing infectiousness relative to the time at which the individual develops symptoms. The drop in infectiousness is due to changes in behaviour when infected individuals develop symptoms. C. Comparison of the fit provided by the two models to data describing serial intervals (the time periods between infectees and their infectors developing symptoms).