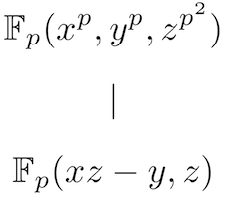Oxford Mathematician Lukas Brantner explains how generalised Lie algebras lead to new insights in Galois theory, deformation theory, and the theory of configuration spaces. Lukas has just been awarded a Royal Society University Research Fellowship. These long term fellowships provide outstanding scientists with the opportunity to build independent research careers and give them the freedom to pursue innovative and transformative scientific research.
"Many celebrated developments in algebraic geometry and topology have progressed in two steps. First, a question is resolved in characteristic zero, e.g. over the real or complex numbers. There, our geometric intuition is sound and the tools of calculus, like exponentials and integrals, are at our disposal. Secondly, new ideas and techniques are introduced to prove an analogue in characteristic $p$ - e.g. over the finite field $\mathbb{F}_p$. This regime is significantly more subtle, because the tools of analysis break down and we cannot divide by $p$, and so expressions like $e^x = \sum_n \frac{x^n}{n!}$ do not make sense.
For an example in algebraic geometry, let $X\subset \mathbb{P}^n(\mathbb{C})$ be a smooth complex manifold defined as the vanishing locus $\left\{f_i(x_0, \ldots, x_n) = 0 \right\}$ of homogeneous polynomials $f_1,\ldots, f_k$. The $i^{th}$ Betti number $b^{\mathbb{C}}_i(X) = \dim_\mathbb{C}(\mathrm{H}^i(X,\mathbb{C}))$ is a good measure for the number of $i$-dimensional holes in $X$; however, some holes can be detected only by $\mathbb{F}_p$-Betti numbers $b_i^{\mathbb{F}_p} = \dim_{\mathbb{F}_p}(\mathrm{H}^i(X,\mathbb{F}_p))$ in characteristic $p$. We can compute the usual Betti numbers $b_i^{\mathbb{C}}(X)$ from the polynomials $f_1, \ldots f_k$ using the so-called de Rham complex, by integrating differential forms along cycles. Recent advances in $p$-adic Hodge theory by Bhatt-Morrow-Scholze show that we can even bound the $\mathbb{F}_p$-Betti numbers $b_i^{\mathbb{F}_p}(X)$ using certain de Rham cohomology groups, provided $X$ is defined over $\mathbb{Q}$ and has good reduction at $p$.
My recent work has followed the paradigm of passing from characteristic $0$ to characteristic $p$ with respect to the following three goals:
(1) Set up a Galois correspondence for general field extensions;
(2) Classify infinitesimal deformations of algebro-geometric objects;
(3) Compute invariants of unordered configuration spaces.
A key ingredient is the theory of partition Lie algebras, a new algebraic structure I have discovered while studying the poset of partitions of $\{1,\ldots n\}$ with its natural action by the symmetric group $\Sigma_n$.
Very informally, partition Lie algebras are generalisations of classical Lie algebras where antisymmetry and the Jacobi identity need not hold on the nose, but only up to coherent homotopy. This means that $[x,[y,z]]$ and $ -[y,[z,x]] - [z,[x,y]]$ need not be equal, but there is a path from the former to the latter.
Formally, partition Lie algebras can either be defined $\infty$-categorically using Goodwillie calculus, which is often helpful in conceptual arguments (cf [BF] [BW]) or $1$-categorically as chain complexes equipped with many operations (cf [BCN]), which has the advantage of being more explicit.
Generalised Lie algebras have several intriguing applications:
(1) Galois Theory. Given a polynomial $f(x)$ with coefficients in a field $K$ of characteristic zero, we can construct a new field $F$ by adding all roots of $f(x)$ to $K$. The Fundamental Theorem of Galois Theory then establishes a one-to-one correspondence between intermediate fields $K\subset E \subset F$ and subgroups $H\subset \mathrm{Gal}(F/K)$ of the group of automorphisms of $F$ fixing $K$. For example, $f(x)= x^4-4x^2+2$ has four real roots $\pm \sqrt{2\pm \sqrt{2}}$, and adding them to $\mathbb{Q}$ gives a new field $F$ for which $\mathrm{Gal}(F/\mathbb{Q})\cong \mathbb{Z}/4\mathbb{Z} $; the subgroup $2\mathbb{Z}/4\mathbb{Z}$ corresponds to the intermediate field $\mathbb{Q}(\sqrt{2})$.
If $f(x)$ has coefficients in a field $K$ of characteristic $p$, the above Galois correspondence often breaks down. For instance, taking the field of rational functions $K=\mathbb{F}_p(T)$ and adjoining a $p^{n}$-th root of $T$, we obtain a nontrivial extension $F/K$ for which the classical Galois group $\mathrm{Gal}(F/K)$ vanishes. This is an example of a purely inseparable extension, meaning that for any $x\in F$, some high power $x^{p^n}$ belongs to $K$. In [BW], Waldron and I generalise the Fundamental Theorem of Galois Theory to the purely inseparable setting, by establishing a correspondence between intermediate fields $K \subset E \subset F$ and subalgebras of the Galois partition Lie algebra $\mathfrak{gal}_{F/K}$ satisfying three simple homological conditions. This generalises an old result of Jacobson from 1944 on extensions $F/K$ satisfying $x^p \in K$ for all $x\in F$.
Figure 1 - A (non-modular) purely inseparable field extension.
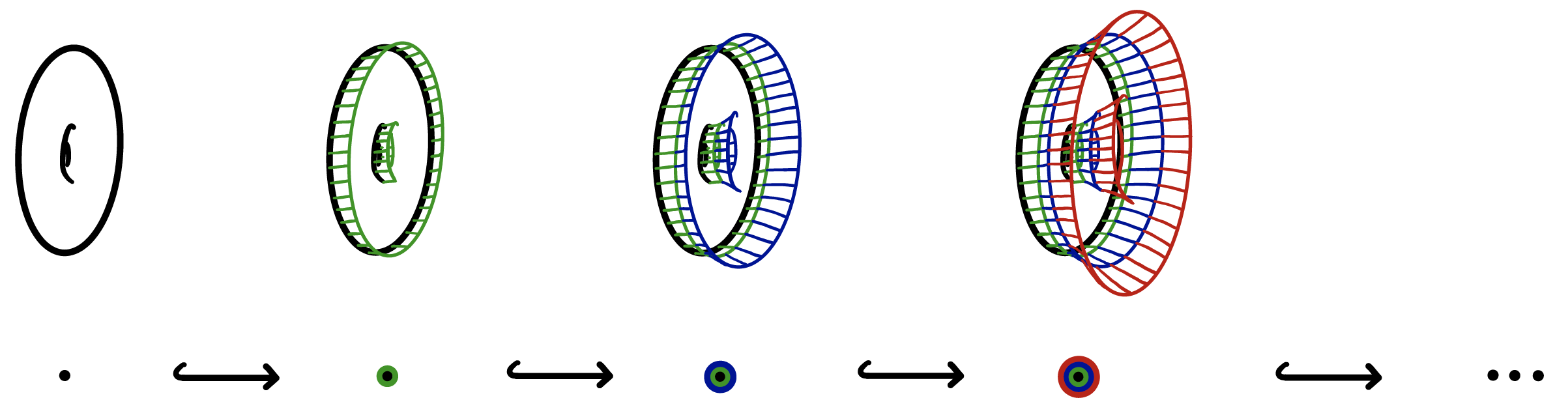
(2) Deformation Theory. Given a smooth projective variety $X$ over the complex numbers, we can study the infinitesimal deformations obtained by varying the defining equations of $X$.
Figure 2 - A sequence of infinitesimal deformations of higher and higher order.
First order deformations of $X$ are classified by the first cohomology group $\mathrm{H}^1(X, T_X)$ of its tangent bundle $T_X$. To formulate a criterion for when first order deformations extend to higher order, we can equip the cohomology $\mathrm{H}^\ast(X,T_X)$ with a Lie bracket, by using the commutator bracket on vector fields. A first order deformation $\widetilde{X} \rightarrow \mathrm{Spec}(\mathbb{C}[\epsilon]/\epsilon^2)$ then extends to higher order precisely if the corresponding class $x\in \mathrm{H}^1(X, T_X)$ satisfies $[x,x] = 0$.
In fact, we can lift the Lie bracket to the so-called Dolbeault complex $$C^\ast(X,{T}_X) = (\ \mathcal{A}^{0,0}({T}_X) \rightarrow \mathcal{A}^{0,1}({T}_X) \rightarrow \mathcal{A}^{0,2}({T}_X) \rightarrow \ \ldots \ ),$$ the homology of which recovers $\mathrm{H}^\ast(X,{T}_X)$. One miracle in Kodaira-Spencer theory is that we can recover all infinitesimal deformations of $X$ from the resulting differential graded Lie algebra, by computing solutions to the Maurer-Cartan equation.
This illustrates a general principle in algebraic geometry, which was discovered by Deligne, Drinfel'd, and Feigin, and later formalised by Lurie and Pridham: infinitesimal deformations of algebro-geometric objects in characteristic zero are controlled by differential graded Lie algebras.
In [BM], Mathew and I generalise this result to characteristic $p$ and beyond, using partition Lie algebras. Infinitesimal deformations in this setting are of particular interest in arithmetic geometry and number theory, for example in the study of deformations of Galois representations. Relying on my work on partition complexes with Arone [AB], we also determine the natural operations acting on the homotopy of partition Lie algebras.
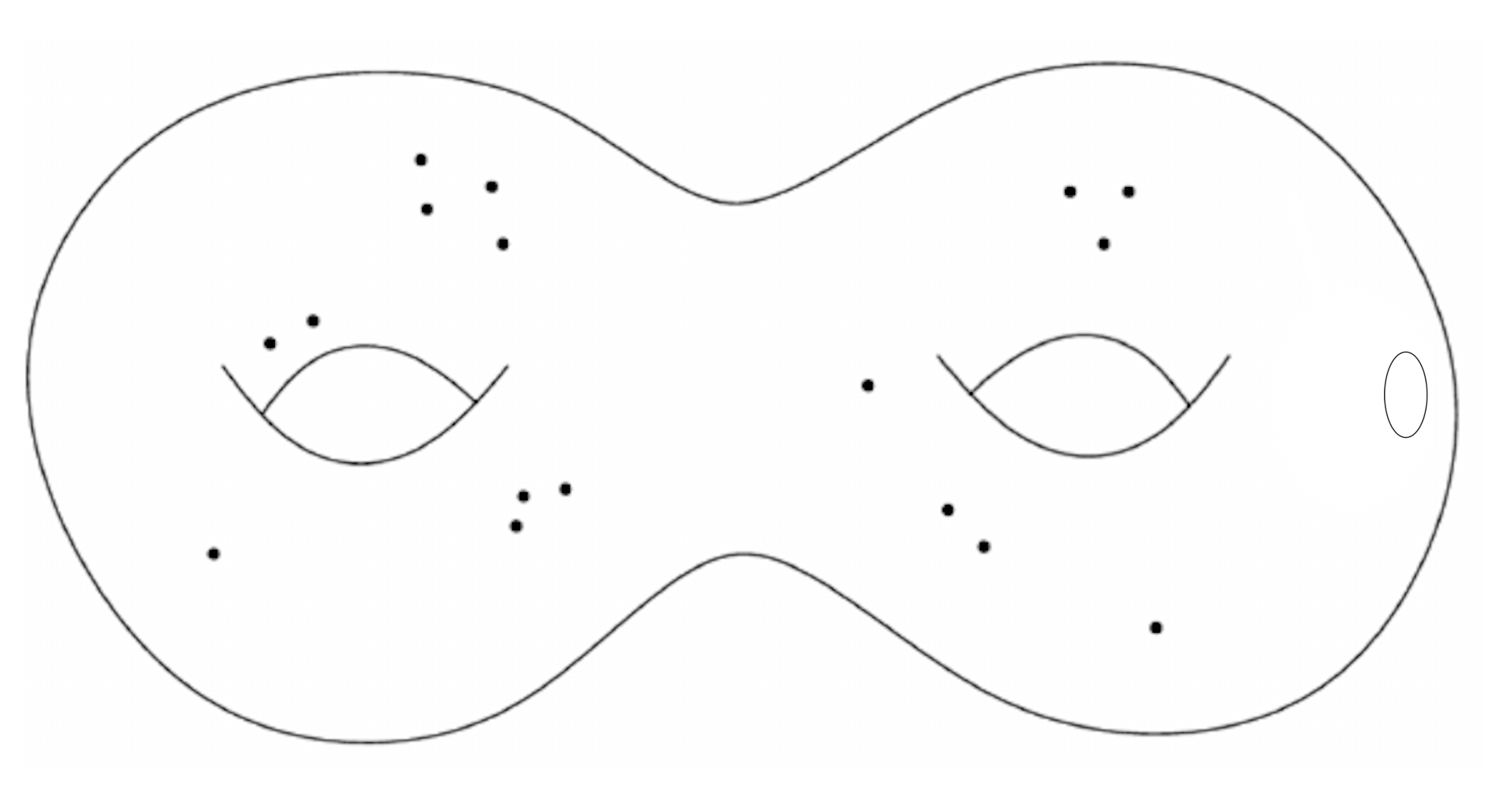
(3) Configuration Spaces. Configuration spaces govern several central objects in mathematics and physics, ranging from loop spaces in topology to Hurwitz spaces in geometry and phase spaces in mechanics. The ordered configuration space of $k$ non-colliding particles in a manifold $M$ is given by $$\mathrm{Conf}_k(M)=\{(x_1,\ldots,x_k) \in M^{k} \ | \ x_i \neq x_j \mbox{ for all } i \neq j\},$$ and the corresponding unordered configuration space is given by the quotient $B_k(M) =\mathrm{Conf}_k(M)/\Sigma_k$.
For example, noting that the location of two non-colliding particles in $\mathbb{R}^3$ is determined by their centre, their distance, and the direction of the line joining them, we find that $\mathrm{Conf}_2(\mathbb{R}^3) = \mathbb{R}^3 \times \mathbb{R}_{>0} \times S^2 \simeq S^2$. Swapping the particles reverses the direction, and so $B_k(\mathbb{R}^3) \simeq S^2/\Sigma_2 \simeq \mathbb{R} P^2$ is the real projective plane.
As we can see in this example, the spaces $B_k(M)$ can be significantly more complicated than the base manifold $M$, and many of their topological properties remain unknown, even in the case of surfaces. The rational cohomology groups $\mathrm{H}^\ast(B_k(M),\mathbb{Q})$, however, are often well-understood.
In my recent paper with Hahn and Knudsen [BHK], we use generalised Lie algebras to access the $\mathbb{F}_p$-cohomology, $K$-theory, and Lubin-Tate theory of configuration spaces, thereby computing several new invariants."
Figure 3: A configuration of points on a surface
Lukas introduces his work in this short film.
[AB] Gregory Arone and Lukas Brantner. The Action of Young Subgroups on the Partition Complex. Publ. Math. Inst. Hautes Etudes Sci., 33:47–156, 2021.
[BCN] Lukas Brantner, Ricardo Campos, and Joost Nuiten. PD Operads and Explicit Partition Lie Algebras. arXiv preprint arXiv:2104.03870, 2021.
[BHK] Lukas Brantner, Jeremy Hahn, and Ben Knudsen. The Lubin–Tate Theory of Configuration Spaces: I. arXiv preprint arXiv:1908.11321, 2020.
[BM] Lukas Brantner and Akhil Mathew. Deformation Theory and Partition Lie Algebras. arXiv preprint arXiv:1904.07352, 2019.
[BW] Lukas Brantner and Joe Waldron. Purely Inseparable Galois Theory I: The Fundamental Theorem. https://arxiv.org/pdf/2010.15707.pdf, 2020.