Industrial inkjets use inkjet technology - familiar to any office printer - to print or deposit materials as part of the manufacturing process of a product on a production line. It requires precise control of the formation and jetting of small droplets of liquid ink.
A typical industrial drop-on-demand (DOD) printhead contains hundreds to thousands of nozzles arranged in an array such that each nozzle can be independently controlled. Nozzle diameters range from 10 to 100 μm in diameter, generating drops with a volume from 0.5 to 500 pL at speeds typically between 5 and 10 m/s.
A key challenge in DOD printing is to identify the combinations of printhead design, actuation signals, and fluid properties to enable the generation of droplets of a specified speed and size while minimizing the formation of satellite droplets. In our paper in 2020, myself, Evangelia Antonopoulou and colleagues, studied the effect of different fluid properties on the break-up. But what if we make it a bit more complicated and consider small agents, called surfactants who move along the interface (and the bulk), and how they affect the surface tension locally? This is our work presented in Physics of Fluids in 2021.
Surfactants are used in many product formulations, including pharmaceuticals, motor oils, and household cleaning products. In recent years, these versatile surface-active agents have found applications in biotechnology, microelectronics, and viral research.
However, jet formation and break-up in inkjet printing has been studied and understood mainly for pure liquids. Questions remain as to the role of surfactants on the inkjet printing process at the microsecond timescale. During my PhD, at University of Leeds, working with Dr Oliver Harlen, Dr Mark Walkley and Professor Nikil Kapur, we investigated the effects of surfactants on jet break-up and drop formation at the scales relevant to drop-on-demand inkjet printing.
In this work we developed a mathematical model capturing the surfactant distribution, coupled with the surface tension change and solved it numerically using the finite element method. We validated our observations against high-quality experiments performed at University of Twente's Physics of Fluids, where we conducted experiments with Maaike Rump and Tim Segers (my PhD project was co-funded by EPSRC CDT in Fluid Dynamics and Ricoh, one of the largest inkjet printing companies).
The flow and surface expansion rates associated with the jetting process are much higher than the typical timescales of surface diffusion and surface adsorbtion of surfactants. Consequently, surfactants are unevenly distributed with a higher concentration on the surface of the drop compared to the ligament. This gives rise to quite different behaviour at the two main break-off events, which are potentially beneficial for inkjet printing.
In order to study the surfactant effect on jetting behaviour we modelled the surfactant distribution along the interface. The effects of surfactants are modelled by introducing a surface tension force in the boundary condition at the free surface that depends upon the surfactant concentration, which in turn requires an additional equation for the surfactant transport at the surface. This transport equation is coupled with a surface tension isotherm, which captures the dependence of the surface tension on the surfactant concentration.
The diffusion of the surfactants on the interface is relatively slow compared to new surface generation and our results show that the surfactants stay at the head of the drop for the first stage of the drop formation and only after the main droplet’s break-off from the ligament is there is a uniform concentration of surfactants on the interface of the droplet. This non-uniformity of the surfactants along the droplet interface gives rise to surface tension gradients and therefore strong Marangoni forces which have a big impact on the jet break-up and drop behaviour.
Figure 1: Surfactants distribution along the newly formed surface. The non-uniform distribution results in Marangoni forces which affect the jet break-up.
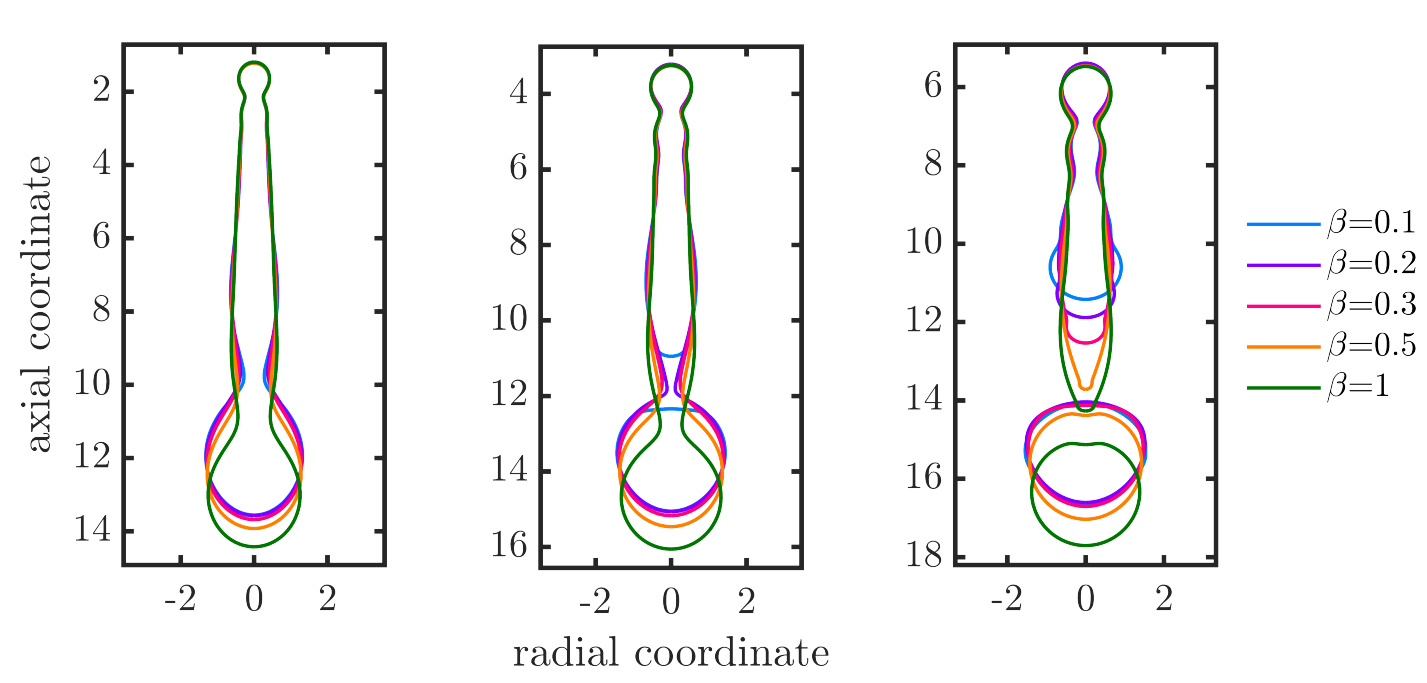
The strength of the surfactant indicates how much the surface tension can be reduced depending on the concentration. Our results show that a stronger surfactant can prevent satellite formation for viscous fluids. This is a consequence of the effect the surfactants have on the thinning rate of the jet neck. We investigated the scaling laws for the jet break-up for different surfactant strengths and our results show that the break-off time of the neck increases with an increasing surfactant strength.
Figure 2: Effect of surfactant strength $\beta$ on the jet break-up. Time increases from left to right.
Although the present study has focused on inkjet printing, where the drop formation is highly controlled, we expected to find similar behaviour for other rapid drop formation processes such as those found in sprays. Here we focused on a simple surfactant-water system. However, our model could in principle be extended to consider fluids with more complex surface rheology, including surface active polymers and biological fluids containing phospholipids or proteins for which dynamic surface tension can be used as a diagnostic tool. In addition to the dilatational interfacial elasticity, these fluids also exhibit a surface stress in response to shear that would need to be incorporated into the model through a constitutive equation for the surface stress.
Figure 3: Numerical simulations against experimental observations. Experiments were conducted at Physics of Fluids, University of Twente with Maaike Rump and Tim Segers.
One of the most common dynamic surface tension measurement methods is the oscillating drop method. However, its use in these microsecond timescales has not yet been investigated with recent works start looking at it experimentally. Using our model for the surfactant distribution and the surface tension computation, we can observe the effect of surfactants on the surface viscosity of the droplets, which so far was assumed negligible since surfactants have no effect on the bulk viscosity; and we can also calculate the surface tension of the droplet in flight and locally. This can be an example of how mathematical modelling can help investigate problems we are yet to understand experimentally.