Holography is one of a set of powerful tools which theoretical physicists use to understand the fundamental aspects of nature. The holographic principle states that the entire information content of a theory of quantum gravity in some volume is equivalent (or dual) to a theory living at the boundary of the volume without gravity. The boundary degrees of freedom encode all the bulk degrees of freedom and their dynamics and vice versa. Understanding the map between the boundary and bulk degrees of freedom leads to a so called duality: whatever we compute on one side gives the exact same result as on the other side, the two descriptions are equivalent. Finding such dualities can be very difficult, and the exact form of the duality is often unknown.
One of the successes of string theory is to give a concrete realisation of the holographic principle via the AdS/CFT correspondence, as conjectured by Juan Maldacena in 1997. Here AdS stands for Anti-de Sitter, the maximally symmetric spacetime with negative cosmological constant, while CFT stands for conformal field theory. A quantum field theory (QFT) is a theoretical framework which physicists use to understand nature, for example the standard model is an example of a quantum field theory. QFTs combine classical field theory, special relativity and quantum mechanics and are used, amongst other things, to make predictions for particle scatterings which are tested at colliders such as at CERN. Conformal symmetry preserve angles but not distances, leading to scale invariant theories. The addition of conformal symmetry to a QFT further constrains the dynamics. The high level of symmetry allows for non-trivial checks of the conjectured correspondence.
One of the most beautiful aspects of the AdS/CFT correspondence is that it is a strong-weak coupling duality. On one side of the duality the theory is weakly coupled and perturbation theory (expanding around a free theory in terms of small coupling constants) may be used, while on the other side the theory is strongly coupled and does not allow for perturbation theory techniques. One can use AdS/CFT to probe the strongly coupled dynamics of a CFT by using its weakly coupled dual gravity description. This has been used successfully to understand QCD at low temperatures, for example the quark-gluon plasma.
A particular class of strongly coupled CFTs, and the focus of my recent research, are the four dimensional $\mathcal{N}=2$ Argyres-Douglas theories. These are inherently strongly coupled theories without a $(\mathcal{N}=2)$ Lagrangian description. There are various ways to realise these theories; the most important for us is their realisation as theories of class $S$ realised as the compactification of a 6d $\mathcal{N}=(2,0)$ theory on a punctured sphere, where one of the two punctures is of irregular or wild type (see figure 1)
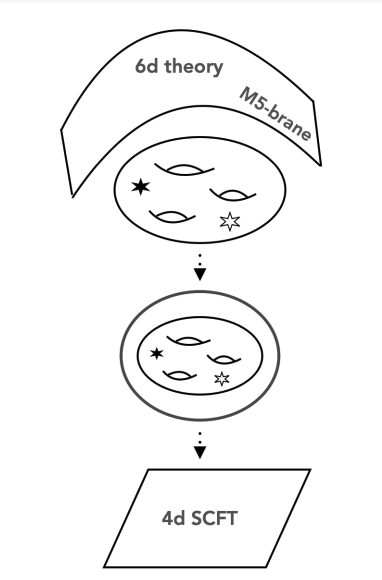
An image describing the compactification of the 6d SCFTs living on M5-branes on a Riemann surface leading to a 4d SCFT
The theories form themselves into families related by Higgs branch renormalisation group flows. Each family has a a parent theory, which is often denoted as $\mathcal{D}_p^b(G)$. Here $G$ is a simple Lie algebra which is a flavour symmetry of the parent theory. The other parameters $b,p$ give information about the irregular puncture. All the other theories in the family can be obtained as the infrared fixed point of a Higgs branch RG flow triggered by giving a nilpotent vacuum expectation value of a moment map of that flavour symmetry. Each theory is then classified by the parent theory $\mathcal{D}_p^b(G)$ and the nilpotent Higgsing, which for our purposes can be encoded in a Young diagram.
In a series of three papers I have investigated different aspects of the holographic duals of these theories. Via AdS/CFT these are expected to be dual to $\mathcal{N}=2$ preserving AdS$_5$ solutions of M-theory. Solutions of this type were classified (the local form of the solutions is given up to solving some differential equations) in a paper by Lin-Lunin-Maldacena. They show that the solutions are governed by a potential $D$ satisfying the SU$(\infty)$ Toda equation. The problem of identifying the holographic duals of these theories is reduced to solving this equation with particular boundary conditions. The boundary conditions that we impose are novel in that they lead to a singular metric. Naively, this would seem to preclude obtaining sensible results. However, it is possible to interpret the singularity as arising due to the presence of smeared M5-branes and from the field theory perspective this is due to the puncture on the sphere in the compactification.
In my first paper on the topic, with collaborators in Korea, I showed how to obtain the solutions for the $\mathcal{D}_p(A)$ theories with arbitrary Higgsing. In the second paper, with Oxford Mathematician Pieter Bomans, Sirui Ning of the Physics Department in Oxford and Yein Lee, a collaborator in Korea, we resolved a small puzzle relating to the existence of broken symmetries in the theory, constructing a more general solution than the previous example. In my third paper on the topic we extended the holographic duality to the arbitrarily Higgsed $\mathcal{D}_p^b(G)$ theories where $G$ is any permissible simple Lie algebra consistent with obtaining a non-trivial theory. We also made contact with work on the field theory side performed by other members of Oxford Mathematics (Chris Beem, Matteo Sacchi and Palash Singh). In their work they showed a redundancy in the description of these AD theories which manifests itself also in the holographic duals. This lead to a nice holographic check of their results and once again showed the power of holography. In each of the papers we were able to compute various observables on the gravity side and check these against known field theory results, finding an impressive matching.
There are a number of open questions that still remain. In particular there are more general AD theories which are called type III, as opposed to type I above. These theories are poorly understood from field theory in comparison to their type I cousins. Using the insights gained from studying their type I cousins from holography we hope to make progress in understanding the type III theories and make predictions beyond what is currently known in field theory. Another interesting connection one can make is to the work on generalised symmetries by other members of Oxford Mathematics (see the article by Dewi Gould). The AD theories studied here have higher form symmetries which we can study holographically too.
This work is based on three articles:
Holographic duals of M5-branes on an irregularly punctured sphere with Hyojoong Kim, Nakwoo Kim, Yein Lee
Symmetry Breaking and Consistent Truncations from M5-branes Wrapping a Disc with Pieter Bomans, Yein Lee, Sirui Ning
Holographic duals of Higgsed $\mathcal{D}_p^b(BCD)$} with Monica Jinwoo Kang, Craig Lawrie and Yein Lee
Christopher Couzens is a Departmental Lecturer in Oxford Mathematics.


