Polynomials Solutions

Part of the Oxford MAT Livestream.

Revision Questions

1. $p(2)=2\times 2^3-5\times 2^2+7\times 2-3=7.$ So $p(2)=7$.
2. We can rearrange to $x^2-x-1=0$ and then use the quadratic formula for $x=\frac{1}{2}\left(1\pm \sqrt{5}\right)$. If we choose the solution with the $+$ sign then we'll get a positive number.
3. In this case, the discriminant "$b^2-4ac$" is $5^2-4\times 2 \times 1=17$.
4. The discriminant for this quadratic is $1-4k$. There are exactly two real solutions if this is positive, which happens when $k<\frac{1}{4}$.
5. This is not a quadratic, but if we change variable by writing $u=x^2$ then we get $u^2-u+k=0$. That's got two real solutions if $k<\frac{1}{4}$, one real solution if $k=\frac{1}{4}$, and no real solutions if $k>\frac{1}{4}$ (thinking about the discriminant again). But let's be careful, because that's the number of solutions there are for $u$, and we really want to know how many solutions there are for $x$.
   If there are no real solutions for $u$ then there can't be any real solutions for $x$. So that rules out $k>\frac{1}{4}$. If there's exactly one solution for $u$ then we might get two real solutions for $x$; they'd be $\pm\sqrt{u}$, but that only works if the solution for $u$ is a positive number. In the case $k=\frac{1}{4}$, we've got one solution for $u$, and if we write down the quadratic formula then that solution is actually $\frac{1}{2}$, so we do get two real solutions for $x$. In the other remaining case $k<\frac{1}{4}$ there are two real solutions for $u$. That could give us as many as four real solutions for $x$. We'd get exactly two real solutions for $x$ if and only if one of the solutions for $u$ is positive and one is negative. Thinking about the factorisation $(u-a)(u-b)$, we can see that the constant term $k$ in our quadratic for $u$ would have to be negative for there to be one positive solution and one negative solution. So we would get two real solutions for $x$ only if $k<0$.
   Putting all that together, there are two real solutions for $x$ if $k<0$ or if $k=\frac{1}{4}$, and for no other values of $k$.
6. The discriminant is $b^2-4$. That's positive (and the quadratic has two real solutions) if $b>2$ or if $b<-2$. If $b=\pm 2$ then the quadratic has one solution. If $-2<b<2$ then the quadratic has no real solutions.
7. If I imagine multiplying out $(x+a)^2$, then I would get a term $2ax$, and I want that to match with the $4x$ term. So I'll take $a=2$. Then if I multiply out $(x+2)^2$, I'd get a term $+4$ at the end; that's not quite what I want, so I'll take $b=-1$ to fix the constant coefficient of this quadratic. I get $(x+2)^2-1$.
8. We can write this polynomial as $-2(x-2)^2+13$. The extreme value is therefore 13. This is a maximum because $-2(x-2)^2\leq 0$.
9. First we're asked to check that $17^3-13\times 17^2-65\times 17-51=0$. To make this easier, don't work out the terms individually. Instead pull out factors of $17$;
   $17^3-13\times 17^2-65\times 17-51=17\left(17^2-13\times 17 -65-3\right)$ because $51=3\times 17$.
   $17^2-13\times 17 -68=17\left(17-13-4\right)$ because $68=4\times 17$.
   $17-13-4=0$ so each line above is equal to zero.
10. By the Factor Theorem, if $p(17)=0$ then $(x-17)$ is a factor of the polynomial. Doing some polynomial division, we can work out that $p(x)=(x-17)(x^2+4x+3)$. We can then write $x^2+4x+3=\left(x+3\right)\left(x+1\right)$ and we've factorised $p(x)$.
11. The polynomial $p(x)$ has a factor of $(x-2)$.
12. We have $p(x)=(x-2)q(x)$ for some polynomial $q(x)$, so $p(2)=(2-2)q(2)=0$.
13. Check that $f(2)=0$.
    Now factorise $f(x)=(x-2)(x^3-4x^2+5x-2)$. Look for more roots; perhaps $x=2$ is a repeated root? In fact $2^3-4\times 2^2+5\times 2-2=0$ so it is a repeated root.
    $f(x)=(x-2)^2(x^2-2x+1)$ and we can recognise that quadratic as $(x-1)^2$.
    So $f(x)=(x-1)^2(x-2)^2$.
14. We might notice that $p(1)=0$. Then write $p(x)=(x-1)(x^2-5x+6)$ and factorise the quadratic for $p(x)=(x-1)(x-2)(x-3)$.
15. $p(3)=-9$ is not zero, so $(x-3)$ is not a factor.
16. Yes, the polynomial could have a repeated root. For example, $p(x)=2(x-1)^2(x-2)$
    • $y=2x^6+x^3+1$. Choosing $u=x^3$ gives $y=2u^3+u+1$.
    • $y=x+\sqrt{2x}$. Choosing $u=\sqrt{x}$ gives $y=u^2+\sqrt{2}u$.
    • $y=3e^{-3x}+6e^{-6x}$. Choosing $u=e^{-3x}$ gives $y=3u+6u^2$.
    • $\displaystyle y=\frac{1+x}{(1-x)^2}$. We can rearrange this to $\displaystyle y=\frac{(x-1)+2}{(1-x)^2}=\frac{-1}{1-x}+\frac{2}{(1-x)^2}$. Choosing $\displaystyle u=\frac{1}{1-x}$ gives $y=-u+2u^2$.
17. $q(x)$ could be $17(x-2)(x+3)(x-1)$ or $39(x-2)^2(x+3)^2(x-1)^2$ or $-(x-3)(x-2)(x-1)x(x+1)(x+2)(x+3)$. We aren't told if these are repeated roots or not, or whether there are any other roots, or what the leading coefficient is.
18. $v(1)=3+a+b$ and that must be zero. Try polynomial division; $$v(x)=(x-1)(x^2+3x+(a+3)),$$ provided that $3+a+b=0$. Now we want $x=1$ to be root of that quadratic, so we need $1+3+a+3=0$. Solve these equations for $a=-7$ and $b=4$.

MAT Questions

MAT 2016 Q1F

• $(x+1)$ is a factor of this polynomial if and only if $-1$ is a root of the polynomial, which would mean that $$(3+(-1)^2)^n-(-1+3)^n(-1-1)^n=0.$$
• This simplifies to $$4^n-2^n(-2)^n=0.$$
• If $n$ is even then $(-2)^n$ is the same as $2^n$ and the equality is true. If $n$ is odd then we have $4^n+4^n$ on the left-hand side, which is not zero for any positive integer $n$.
• So the answer is (b).

MAT 2015 Q1I

• Here's a sketch
   

  

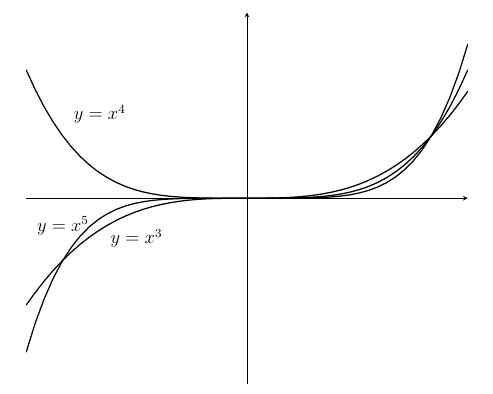
• The three curves all pass through $(0,0)$ and $(1,1)$. The curves $y=x^3$ and $y=x^5$ both pass through $(-1,-1)$.
• There's one region above all three curves, one region below all three curves, and a total of seven regions between the curves.
• The answer is (d).

MAT 2007 Q2

(i) Plugging in $n=3$, we have $f_3(x)=(\left(2+(-2)^3\right))x^2+(3+3)x+3^2=-6x^2+6x+9$.

Completing the square, we can write this as $\displaystyle -6\left(x-\frac{1}{2}\right)^2+\frac{21}{2}$

The polynomial is usually a quadratic (unless the leading coefficient $2+(-2)^n$ happens to be zero), in which case it has a maximum if and only if the leading coefficient is negative (if it's a ``sad" quadratic), which happens if $n$ is odd. Watch out for the special case though; $2+(-2)^n$ is zero if $n=1$, in which case the polynomial is a linear function without a maximum.

(ii) $f_1(x)=4x+1$.

$f_1(f_1(x))=4(4x+1)+1=4^2 x+4+1=16x+5$.

$f_1(f_1(f_1(x)))=4(4^2x+4+1)+1=4^3x+16+4+1=64x+21$

In general, $f_1(f_1(\cdots f_1(x)\cdots))$ with $f_1$ applied $k$ times is equal to $4^k x+4^{k-1}+4^{k-2}+\dots+4+1$.

The constant term is a geometric series, so we can simplify to $$4^k x+ \frac{4^k-1}{4-1}=4^k x +\frac{4^k-1}{3}.$$

(iii) $f_2(x)=6x^2+5x+4$ is a quadratic. Each time we repeatedly square, the degree gets multiplied by 2. So the degree of $f_2(f_2(\cdots f_2(x)\cdots))$ with $f_2$ applied $k$ times is $2^k$.

Extension

• $f_n(x)$ with $n>2$ is still a quadratic, so the degree of $f_n(f_n(\cdots f_n(x)\cdots))$ with $f_n$ applied $k$ times is $2^k$ just like in the last part of the question.
• Let's look at what happens for $f(x)=ax^2$ for real non-zero $a$ (only the highest power really matters for this question). $f(f(x))=a(ax^2)^2=a^3x^4$ and $f(f(f(x)))=a(a^3x^4)^2=a^7x^8$, so it looks like the coefficient of $x^{2^k}$ is $a^{2^k-1}$. For the quadratic we're talking about here, the coefficient ends up being $(2+(-2)^n)^{2^k-1}$.
• For $n$ odd and greater than 3, $g$ is a quadratic with a maximum value. $n=3$ is special; $g_3(x)=9$. That has a maximum value of 9 (which is happens to take for all $x$).
• For $n\neq 3$ the degree is $2^k$ again. For $n=3$ the degree is zero because the outcome after all those function applications is still just the value 9.

MAT 2011 Q2

(i) Multiply both sides by $x$ to get $x^4=2x^2+x$.

Then multiply both sides by $x$ again for $x^5=2x^3+x^2$. Now use the fact that $x^3=2x+1$ to write
$x^5=2(2x+1)+x^2=2+4x+x^2$.

(ii) In general we can multiply by $x$ and use the initial fact about $x^3$ to remove any $x^3$ term we get. In general, it looks like this;
$$x^{k+1}=\left(x^k\right)x=\left(A_k+B_k x + C_k x^2\right)x=A_k x + B_k x^2 + C_k x^3 = A_k x + B_k x^2 + C_k \left(2x+1\right).$$
Now remember that $x^{k+1}=A_{k+1}+B_{k+1}x+C_{k+1}x^2$. We can match this up  with the expression on the right by taking $A_{k+1}=C_k$ and $B_{k+1}=A_k+2C_k$ and $C_{k+1}=B_k$.

(iii) By the previous part, $$A_{k+1}+C_{k+1}-B_{k+1}=C_k+B_k-(A_k+2C_k).$$
That simplifies to $B_k-A_k-C_k$. So $D_{k+1}=-D_k$.

We can also note that $D_4=1$, so $D_5=-1$ and $D_6=1$ and so on; we have $D_k=(-1)^k$. Then use the definition of $D_k$ and rearrange $A_k+C_k-B_k=(-1)^k$ by adding $B_k$ to both sides.

(iv) We're asked to show that $A_{k+1}+C_{k+1}+A_{k+2}+C_{k+2}=A_{k+3}+C_{k+3}$. The way to approach this which is clearest to me is to use the previous part to replace the $A_{k+3}$ and $C_{k+3}$ for things with subscript $k+2$, then replace everything that has a subscript $k+2$ for things with subscript $k+1$, and then hope that everything balances.

I have $A_{k+1}+C_{k+1}+(A_{k+2}+C_{k+2})=A_{k+1}+C_{k+1}+(C_{k+1}+B_{k+1})$ on the left.

I have $A_{k+3}+(C_{k+3})=C_{k+2}+(B_{k+2})=B_{k+1}+(A_{k+1}+2C_{k+1})$ on the right.

[The brackets here are just to make it clearer which terms I'm replacing with which.]

These are equal, so the fact is true.

Alternatively, replace the $A_k+C_k$ terms with $B_k+(-1)^k$ and go from there.
 

Extension

• Given $x^2=x+1$, we could multiply both sides by $x$ for $x^3=x^2+x$, then replace the $x^2$ for $x+1$ to get $x^3=2x+1$. The roots of that quadratic are $\displaystyle x=\frac{1\pm \sqrt{5}}{2}$. The other solution to $x^3=2x+1$ is $x=-1$.
  The quantity $D_k$ is just the value of the quadratic at $x=-1$, and so we have $$A_k+B_k(-1)+C_k(-1)^2=(-1)^k.$$