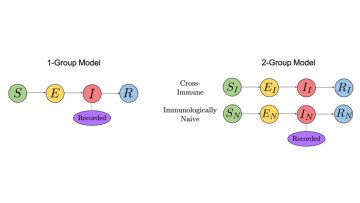
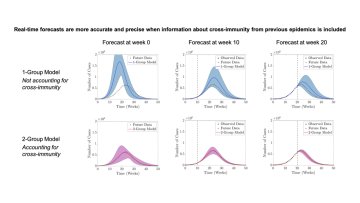
Extensions of Functions - Lecture 2 of 4
4 x 1.5 hour Lectures
Aimed at: any DPhil students with interest in learning about extensions of functions.
Suggested Pre-requisites: Suitable for OxPDE students, but also of interests to functional analysts, geometers, probabilists, numerical analysts and anyone who has a suitable level of prerequisite knowledge.
Abstract
Abstract. The aim of the course is to present several results on extensions of functions. Among the most important are Kirszbraun's and Whitney's theorems.
They provide powerful technical tools in many problems of analysis. One way to view these theorems is that they show that there exists an interpolation
of data with certain properties. In this context they are useful in computer science, e.g. in clustering of data (see e.g. [26, 23]) and in dimension reduction (see e.g. [15]).
1. Syllabus
Lecture 1. McShane's theorem [25], Kirszbraun's theorem [18, 31, 35], Kneser- Poulsen conjecture [19, 29, 16].
Lecture 2. Whitney's covering and associated partition of unity, Whitney's ex-tension theorem [37, 12, 33].
Lecture 3. Whitney's theorem { minimal Lipschitz extensions [22].
Lecture 4. Ball's extension theorem, Markov type and cotype [6].
2. Required mathematical background
Markov chains, Hilbert spaces, Banach spaces, metric spaces, Zorn lemma
3. Reading list
The reading list consists of all the papers cited above, lecture notes [27], and parts of books [36, 8].
4. Assesment
Students will be encouraged to give a short talk on a topic related to the content of the course. Suggested topics include:
(1) Brehm's theorem [10],
(2) continuity of Kirszbraun's extension theorem [20],
(3) Kirszbraun's theorem for Alexandrov spaces [21, 1],
(4) two-dimensional Kneser-Poulsen conjecture [9],
(5) origami [11],
(6) absolutely minimising Lipschitz extensions and innity Laplacian [17, 32,
34, 2, 3, 5, 4],
(7) Fenchel duality and Fitzpatrich functions [30, 7],
(8) sharp form of Whitney's extension theorem [13],
(9) Whitney's extension theorem for Cm [14],
(10) Markov type and cotype calculation [27, 6, 28],
(11) extending Lipschitz functions via random metric partitions [24, 27].
References
1. S. Alexander, V. Kapovitch, and A. Petrunin, Alexandrov meets Kirszbraun, 2017.
2. G. Aronsson, Minimization problems for the functional supx F(x; f(x); f0(x)), Ark. Mat. 6 (1965), no. 1, 33{53.
3. , Minimization problems for the functional supx F(x; f(x); f0(x))(ii), Ark. Mat. 6 (1966), no. 4-5, 409{431.
4. , Extension of functions satisfying lipschitz conditions, Ark. Mat. 6 (1967), no. 6, 551{561.
5. , Minimization problems for the functional supx F(x; f(x); f0(x))(iii), Ark. Mat. 7 (1969), no. 6, 509{512.
6. K. Ball, Markov chains, Riesz transforms and Lipschitz maps, Geometric & Functional Analysis GAFA 2 (1992), no. 2, 137{172.
7. H. Bauschke, Fenchel duality, Fitzpatrick functions and the extension of rmly nonexpansive mappings, Proceedings of the American Mathematical Society 135 (2007), no. 1, 135{139. MR 2280182
8. Y. Benyamini and J. Lindenstrauss, Geometric nonlinear functional analysis, Colloquium publications (American Mathematical Society) ; v. 48, American Mathematical Society, Providence, R.I., 2000 (eng).
9. K. Bezdek and R. Connelly, Pushing disks apart { the Kneser-Poulsen conjecture in the plane, Journal fur die reine und angewandte Mathematik (2002), no. 553, 221 { 236.
10. U. Brehm, Extensions of distance reducing mappings to piecewise congruent mappings on Rm, J. Geom. 16 (1981), no. 2, 187{193. MR 642266
11. B. Dacorogna, P. Marcellini, and E. Paolini, Lipschitz-continuous local isometric immersions: rigid maps and origami, Journal de Mathematiques Pures et Appliques 90 (2008), no. 1, 66 { 81.
12. L. C. Evans and R. F. Gariepy, Measure theory and ne properties of functions; Rev. ed., Textbooks in mathematics, ch. 6, CRC Press, Oakville, 2015.
13. C. L. Feerman, A sharp form of Whitney's extension theorem, Annals of Mathematics 161 (2005), no. 1, 509{577. MR 2150391
14. , Whitney's extension problem for Cm, Annals of Mathematics 164 (2006), no. 1, 313{359. MR 2233850
15. L.-A. Gottlieb and R. Krauthgamer, A nonlinear approach to dimension reduction, Weizmann Institute of Science.
16. M. Gromov, Monotonicity of the volume of intersection of balls, Geometrical Aspects of Functional Analysis (Berlin, Heidelberg) (J. Lindenstrauss and V. D. Milman, eds.), Springer Berlin Heidelberg, 1987, pp. 1{4.
17. R. Jensen, Uniqueness of Lipschitz extensions: Minimizing the sup norm of the gradient, Archive for Rational Mechanics and Analysis 123 (1993), no. 1, 51{74.
18. M. Kirszbraun, Uber die zusammenziehende und Lipschitzsche Transformationen, Fundamenta Mathematicae 22 (1934), no. 1, 77{108 (ger).
19. M. Kneser, Einige Bemerkungen uber das Minkowskische Flachenma, Archiv der Mathematik 6 (1955), no. 5, 382{390.
20. E. Kopecka, Bootstrapping Kirszbraun's extension theorem, Fund. Math. 217 (2012), no. 1, 13{19. MR 2914919
21. U. Lang and V. Schroeder, Kirszbraun's theorem and metric spaces of bounded curvature, Geometric & Functional Analysis GAFA 7 (1997), no. 3, 535{560. MR 1466337
22. E. Le Gruyer, Minimal Lipschitz extensions to dierentiable functions dened on a Hilbert space, Geometric and Functional Analysis 19 (2009), no. 4, 1101{1118. MR 2570317
23. J. Lee, Jl lemma and Kirszbraun's extension theorem, 2020, Sublinear Algorithms for Big Data Lectues Notes, Brown University.
24. J. R. Lee and A. Naor, Extending Lipschitz functions via random metric partitions, Inventiones mathematicae 160 (2005), no. 1, 59{95.
25. E. J. McShane, Extension of range of functions, Bull. Amer. Math. Soc. 40 (1934), no. 12, 837{842. MR 1562984
26. A. Naor, Probabilistic clustering of high dimensional norms, pp. 690{709.
27. , Metric embeddings and Lipschitz extensions, Princeton University, Lecture Notes, 2015.
28. A. Naor, Y. Peres, O. Schramm, and S. Sheeld, Markov chains in smooth Banach spaces and Gromov-hyperbolic metric spaces, Duke Math. J. 134 (2006), no. 1, 165{197.
29. E. T. Poulsen, Problem 10, Mathematica Scandinavica 2 (1954), 346.
30. S. Reich and S. Simons, Fenchel duality, Fitzpatrick functions and the Kirszbraun{Valentine extension theorem, Proceedings of the American Mathematical Society 133 (2005), no. 9, 2657{2660. MR 2146211
31. I. J. Schoenberg, On a Theorem of Kirzbraun and Valentine, The American Mathematical Monthly 60 (1953), no. 9, 620{622. MR 0058232
32. S. Sheeld and C. K. Smart, Vector-valued optimal Lipschitz extensions, Communications on Pure and Applied Mathematics 65 (2012), no. 1, 128{154. MR 2846639
33. E. Stein, Singular integrals and dierentiability properties of functions, ch. 6, Princeton University Press, 1970.
34. P. V. Than, Extensions lipschitziennes minimales, Ph.D. thesis, INSA de Rennes, 2015.
35. F. A. Valentine, A Lipschitz condition preserving extension for a vector function, Amer. J. Math. 67 (1945), 83{93. MR 0011702
36. J. H. Wells and L. R. Williams, Embeddings and extensions in analysis, Ergebnisse der Mathematik und ihrer Grenzgebiete ; Bd. 84, Springer-Verlag, Berlin, 1975 (eng).
37. H. Whitney, Analytic extensions of dierentiable functions dened in closed sets, Transactions of the American Mathematical Society 36 (1934), no. 1, 63{89. MR 1501735
University of Oxford, Mathematical Institute and St John's College, Oxford, United Kingdom
E-mail address: @email