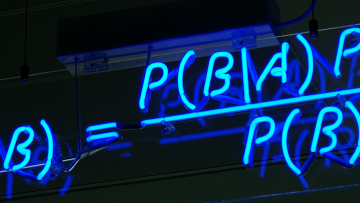When one wants to describe the symmetries of any object or system, in mathematics or everyday life, the right language to use is group theory. How might one go about understanding the universe of all groups and what kinds of novel geometry might emerge as we explore this universe?
![""](/system/files/styles/medium/private/articles/images/ada.png?h=b4c164b4&itok=rilIN9sL """")
When you think about the founders of computing you may think Alan Turing, you may even think Charles Babbage. But you should definitely think about Ada Lovelace. Ada Lovelace is not only the link between Babbage and Turing, but a woman of fierce originality and intellectual interests whose ideas went beyond Babbage’s ideas of computers as manipulating numbers, and focused on their creative possibilities and their limits, the very issues with which we are wrestling today.
12:00
Concentration Compactness for the Critical Maxwell-Klein-Gordon Equation
Abstract
12:00
Regularity of level sets and flow lines
Abstract
Humans love to find an explanation that fits the facts, and fits them as closely as possible. But this often turns out to be a terrible way of learning about the world around us.
In the latest instalment of the Oxford Mathematics Alphabet we look at Bayes’ Theorem and how it is used in criminology, product recommendations, artificial intelligence, and recently in the search for the missing Malaysian Airliner MH370.
Strongly semistable sheaves and the Mordell-Lang conjecture over function fields
Abstract
We shall describe a new proof of the Mordell-Lang conjecture in positive characteristic, in the situation where the variety under scrutiny is a smooth subvariety of an abelian variety.
Our proof is based on the theory of semistable sheaves in positive characteristic, in particular on Langer's theorem that the Harder-Narasimhan filtration of sheaves becomes strongly semistable after a finite number of iterations of Frobenius pull-backs. Our proof produces a numerical upper-bound for the degree of the finite morphism from an isotrivial variety appearing in the statement of the Mordell-Lang conjecture. This upper-bound is given in terms of the Frobenius-stabilised slopes of the cotangent bundle of the variety.
(Joint Number Theory and Logic) On a modular Fermat equation
Abstract
I will describe some diophantine problems and results motivated by the analogy between powers of the modular curve and powers of the multiplicative group in the context of the Zilber-Pink conjecture.