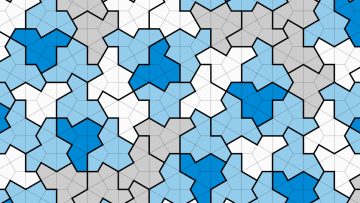
We will be celebrating the discovery of 'The Hat', a tile which tiles only aperiodically, on the 20th and 21st July here in the Mathematical Institute, Oxford. Come and join us!
The theory of tilings in the plane touches on diverse areas of mathematics, physics and beyond. Aperiodic sets of tiles, such as the famous Penrose tiling that you see as you walk into the Mathematical Institute, admit tilings of the plane without any translational symmetry.