12:30
12:30
12:30
Quantization of Bandlimited Graph Signals
Abstract
Graph signals provide a natural representation of data in many applications, such as social networks, web information analysis, sensor networks, and machine learning. Graph signal & data processing is currently an active field of mathematical research that aims to extend the well-developed tools for analyzing conventional signals to signals on graphs while exploiting the underlying connectivity. A key challenge in this context is the problem of quantization, that is, finding efficient ways of representing the values of graph signals with only a finite number of bits.
In this talk, we address the problem of quantizing bandlimited graph signals. We introduce two classes of noise-shaping algorithms for graph signals that differ in their sampling methodologies. We demonstrate that these algorithms can efficiently construct quantized representatives of bandlimited graph-based signals with bounded amplitude.
Inspired by the results of Zhang et al. in 2022, we provide theoretical guarantees on the relative error between the true signal and its quantized representative for one of the algorithms.
As will be discussed, the incoherence of the underlying graph plays an important role in the quantization process. Namely, bandlimited signals supported on graphs of lower incoherence allow for smaller relative errors. We support our findings with various numerical experiments showcasing the performance of the proposed quantization algorithms for bandlimited signals defined on graphs with different degrees of incoherence.
This is joint work with Felix Krahmer (Technical University of Munich), He Lyu (Meta), Rayan Saab (University of California San Diego), and Rongrong Wang (Michigan State University).
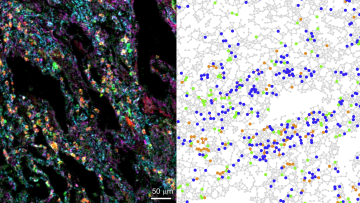
Mathematical modelling played a key role in describing the spread of the COVID-19 pandemic; now a different kind of maths is helping us understand how immune cells interact in the lungs of patients with severe COVID-19.
In a damaged lung with a massive immune cell infiltrate, as seen with severe COVID-19 infection, it can be difficult to figure out which cells are involved in causing lung injury.
Modeling multiscale systems in bone mechanobiology
Abstract
Bone regeneration processes are complex multiscale intrinsic mechanisms in bone tissue whose primary outcome is restoring function and form to a bone insufficiency. The effect of mechanics on the newly formed bone (the woven bone), is fundamental, at the tissue, cellular or even molecular scale. However, at these multiple scales, the identification of the mechanical parameters and their mechanisms of action are still unknown and continue to be investigated. This concept of mechanical regulation of biological processes is the main premise of mechanobiology and is used in this seminar to understand the multiscale response of the woven bone to mechanical factors in different bone regeneration processes: bone transport, bone lengthening and tissue engineering. The importance of a multidisciplinary approach that includes both in vivo and in silico modeling will be remarked during the seminar.
Extreme pushed and pulled fronts
Abstract
I shall say some stuff about quasilinear reaction-diffusion equations, motivated by tissue growth in particular.
OCIAM-WCMB SEMINAR Structural identifiability analysis: An important tool in systems modelling
Abstract
For many systems (certainly those in biology, medicine and pharmacology) the mathematical models that are generated invariably include state variables that cannot be directly measured and associated model parameters, many of which may be unknown, and which also cannot be measured. For such systems there is also often limited access for inputs or perturbations. These limitations can cause immense problems when investigating the existence of hidden pathways or attempting to estimate unknown parameters and this can severely hinder model validation. It is therefore highly desirable to have a formal approach to determine what additional inputs and/or measurements are necessary in order to reduce or remove these limitations and permit the derivation of models that can be used for practical purposes with greater confidence.
Structural identifiability arises in the inverse problem of inferring from the known, or assumed, properties of a biomedical or biological system a suitable model structure and estimates for the corresponding rate constants and other model parameters. Structural identifiability analysis considers the uniqueness of the unknown model parameters from the input-output structure corresponding to proposed experiments to collect data for parameter estimation (under an assumption of the availability of continuous, noise-free observations). This is an important, but often overlooked, theoretical prerequisite to experiment design, system identification and parameter estimation, since estimates for unidentifiable parameters are effectively meaningless. If parameter estimates are to be used to inform about intervention or inhibition strategies, or other critical decisions, then it is essential that the parameters be uniquely identifiable.
Numerous techniques for performing a structural identifiability analysis on linear parametric models exist and this is a well-understood topic. In comparison, there are relatively few techniques available for nonlinear systems (the Taylor series approach, similarity transformation-based approaches, differential algebra techniques and the more recent observable normal form approach and symmetries approaches) and significant (symbolic) computational problems can arise, even for relatively simple models in applying these techniques.
In this talk an introduction to structural identifiability analysis will be provided demonstrating the application of the techniques available to both linear and nonlinear parameterised systems and to models of (nonlinear mixed effects) population nature.