14:30
14:30
14:00
Finite element approximation of implicitly constituted incompressible flow models
14:30
Multi-index methods for quadrature
Abstract
Multi-index methods are a generalization of multilevel methods in high dimensional problem and are based on taking mixed first-order differences along all dimensions. With these methods, we can accurately and efficiently compute a quadrature or construct an interpolation where the integrand requires some form of high dimensional discretization. Multi-index methods are related to Sparse Grid methods and the Combination Technique and have been applied to multiple sampling methods, i.e., Monte Carlo, Stochastic Collocation and, more recently, Quasi Monte Carlo.
In this talk, we describe and analyse the Multi-Index Monte Carlo (MIMC) and Multi-Index Stochastic Collocation (MISC) methods for computing statistics of the solution of a PDE with random data. Provided sufficient mixed regularity, MIMC and MISC achieve better complexity than their corresponding multilevel methods. We propose optimization procedures to select the most effective mixed differences to include in these multi-index methods. We also observe that in the optimal case, the convergence rate of MIMC and MISC is only dictated by the convergence of the deterministic solver applied to a one-dimensional spatial problem. We finally show the effectiveness of MIMC and MISC in some computational tests, including PDEs with random coefficients and Stochastic Particle Systems.
17:00
“Knowledge gained by experience”: Olaus Henrici – engineer, geometer, and maker of mathematical models
Abstract
The (Danish-born) German mathematician Olaus Henrici (1840–1918) studied in Karlsruhe, Heidelberg and Berlin before making his career in London, first at University College and then, from 1884, at the newly formed Central Technical College where he established a Laboratory of Mechanics. Although Henrici’s original training was as an engineer, he became known as a promoter of projective geometry and as an advocate for the use of mathematical models. In my talk, I shall discuss the different aspects of Henrici's work and explore connections between them.
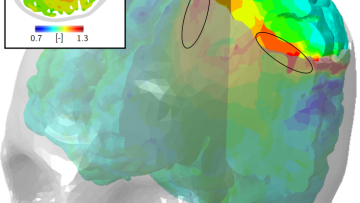
For over a hundred years, when confronted by swelling in the brain, surgeons more often than not have resorted to decompressive craniectomy, the traditional route to reducing swelling by removing a large part of the skull. However, while this might be the standard procedure, its failure rate has been worryingly high, primarily because the consequences on the rest of the brain have been poorly understood.
16:00
Random waves on the three-dimensional torus and correlations of spherical lattice points
Abstract
I will discuss some recent work, joint with R. Maffucci, concerning random Laplace eigenfunctions on the torus T^3=R^3/Z^3. Studying various statistics of these 'random waves' we will be confronted with an arithmetic question about linear relations among integer points on spheres.
16:00
On the standard L-function attached to Siegel-Jacobi modular forms of higher index
Abstract
In this talk we will start by introducing the notion of Siegel-Jacobi modular form and explain its close relation to Siegel modular forms through the Fourier-Jacobi expansion. Then we will discuss how one can attach an L-function to an appropriate (i.e. eigenform) Siegel-Jacobi modular form due to Shintani, and report on joint work with Jolanta Marzec on analytic properties of this L-function, extending results of Arakawa and Murase.
16:00
Correlations of multiplicative functions
Abstract
We develop the asymptotic formulas for correlations
\[ \sum_{n\le x}f_1(P_1(n))f_2(P_2(n))\cdot \dots \cdot f_m(P_m(n))\]
where $f_1,\dots,f_m$ are bounded ``pretentious" multiplicative functions, under certain natural hypotheses. We then deduce several desirable consequences: first, we characterize all multiplicative functions $f:\mathbb{N}\to\{-1,+1\}$ with bounded partial sums. This answers a question of Erd{\"o}s from $1957$ in the form conjectured by Tao. Second, we show that if the average of the first divided difference of multiplicative function is zero, then either $f(n)=n^s$ for $\operatorname{Re}(s)<1$ or $|f(n)|$ is small on average. This settles an old conjecture of K\'atai. Third, we discuss applications to the study of sign patterns of $(f(n),f(n+1),f(n+2))$ and $(f(n),f(n+1),f(n+2),f(n+3))$ where $f:\mathbb{N}\to \{-1,1\}$ is a given multiplicative function. If time permits, we discuss multidimensional version of some of the results mentioned above.
16:00
Effective equidistribution of rational points on expanding horospheres
Abstract
The equidistribution theorem for rational points on expanding horospheres with fixed denominator in the space of d-dimensional Euclidean lattices has been derived in the work by M. Einsiedler, S. Mozes, N. Shah and U. Shapira. The proof of their theorem requires ergodic theoretic tools, including Ratner's measure classification theorem. In this talk I will present an alternative approach, based on harmonic analysis and Weil's bound for Kloosterman sums. In the case of d=3, unlike the ergodic-theoretic approach, this provides an explicit estimate on the rate of convergence. This is a joint work with Jens Marklof.
16:00
Arithmetic applications of $\omega$-integral curves in varieties (Joint with Logic)
Abstract
In 2000, Vojta solved the n-squares problem under the Bombieri-Lang conjecture, by explicitly finding all the curves of genus 0 or 1 on the surfaces related to this problem. The fundamental notion used by him is $\omega$-integrality of curves.
In this talk, I will show a generalization of Vojta's method to find all curves of low genus in some surfaces, with arithmetic applications.
I will also explain how to use $\omega$-integrality to obtain a bound of the height of a non-constant morphism from a curve to $\mathbb{P}^2$ in terms of the number of intersections (without multiplicities) of its image with a divisor of a particular kind.
This proves some new special cases of Vojta's conjecture for function fields.