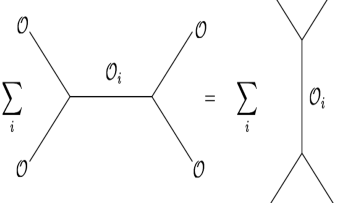
What does boiling water have in common with magnets and the horizon of black holes? They are all described by conformal field theories (CFTs)! We are used to physical systems that are invariant under translations and rotations. Imagine a system which is also invariant under scale transformations. Such a system is described by a conformal field theory. Remarkably, many physical systems admit such a description and conformal field theory is ubiquitous in our current theoretical understanding of nature.
Modular Structure in Temporal Protein Interaction Networks
Abstract
Protein interaction networks (PINs) allow the representation and analysis of biological processes in cells. Because cells are dynamic and adaptive, these processes change over time. Thus far, research has focused either on the static PIN analysis or the temporal nature of gene expression. By analysing temporal PINs using multilayer networks, we want to link these efforts. The analysis of temporal PINs gives insights into how proteins, individually and in their entirety, change their biological functions. We present a general procedure that integrates temporal gene expression information with a monolayer PIN to a temporal PIN and allows the detection of modular structure using multilayer modularity maximisation.
Interfaces in a spatial population model
Abstract
We consider the symbiotic branching model, which describes a spatial population consisting of two types in terms of a coupled system of stochastic PDEs. One particularly important special case is Kimura's stepping stone model in evolutionary biology. Our main focus is a description of the interfaces between the types in the large scale limit of the system. As a new tool we will introduce a moment duality, which also holds for the limiting model. This also has implications for a classification of entrance laws of annihilating Brownian motions.