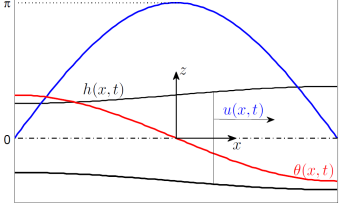
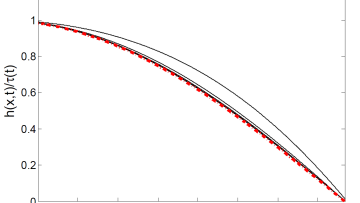
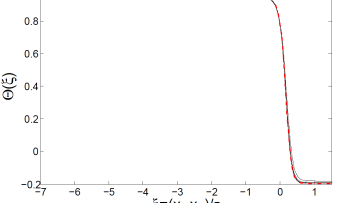
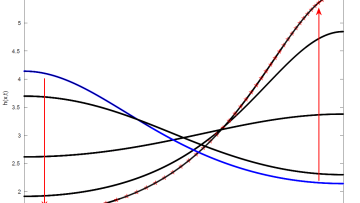
Free suspended liquid films or sheets are often formed during industrial production of sprays as well as in natural processes such as sea spray. Early experimental and theoretical investigations of them were done by French physicist Felix Savart, who observed liquid sheets forming by a jet impact on a solid surface, or by two jets impacting each other (1833), and British physicist Arthur Mason Worthington, a pioneer in investigation of the crown splash forming after impact of a drop onto a liquid surface.
12:45
Loop Amplitudes in the Scattering Equations Formalism
Abstract
I will describe recent progress in the study of scattering amplitudes in gauge theory and gravity at loop level, using the formalism of the scattering equations. The scattering equations relate the kinematics of the scattering of massless particles to the moduli space of the sphere. Underpinned by ambitwistor string theory, this formalism provides new insights into the relation between tree-level and loop-level contributions to scattering amplitudes. In this talk, I will describe results up to two loops on how loop integrands can be constructed as forward-limits of trees. One application is the loop-level understanding of the colour-kinematics duality, a symmetry of perturbative gauge theory which relates it to perturbative gravity.
12:45
Modular graph functions as iterated Eisenstein integrals
Abstract
Superstring scattering amplitudes in genus one have a low-energy expansion in terms of certain real analytic modular forms, called modular graph functions (D'Hoger, Green, Gürdogan and Vanhove). I will sketch the proof that these functions belong to a family of iterated integrals of modular forms (a generalization of Eichler integrals), recently introduced by Francis Brown, which explains many of their properties. The main tools are elliptic multiple polylogarithms (Brown and Levin), single-valued versions thereof, and elliptic multiple zeta values (Enriquez).
16:00
On decidability in local and global fields
Abstract
This is a survey on recent advances in classical decidability issues for local and global fields and for some canonical infinite extensions of those.
16:00
Cubulating Groups
Abstract
Cubulating a group means finding a proper cocompact action on a CAT(0) cube complex. I will describe how cubulating a group tells us some nice properties of the group, and explain a general strategy for finding cubulations.
11:00
Hilbert's 10th Problem: What We Know and What We Don't
Abstract
In this talk I will introduce Hilbert's 10th Problem (H10) and the model-theoretic notions necessary to explore this problem from the perspective of mathematical logic. I will give a brief history of its proof, talk a little about its connection to decidability and definability, then close by speaking about generalisations of H10 - what has been proven and what has yet to be discovered.
Polya’s Program for the Riemann Hypothesis and Related Problems
Abstract
In 1927 Polya proved that the Riemann Hypothesis is equivalent to the hyperbolicity of Jensen polynomials for Riemann’s Xi-function. This hyperbolicity has only been proved for degrees d=1, 2, 3. For each d we prove the hyperbolicity of all but (perhaps) finitely many Jensen polynomials. We obtain a general theorem which models such polynomials by Hermite polynomials. This theorem also allows us to prove a conjecture of Chen, Jia, and Wang on the partition function. This result can be thought of as a proof of GUE for the Riemann zeta function in derivative aspect. This is joint work with Michael Griffin, Larry Rolen, and Don Zagier.
Multizeta and related algebraic structures in the function field arithmetic
Abstract
We will see some results and conjectures on the zeta and multizeta values in the function field context, and see how they relate to homological-homotopical objects, such as t-motives, iterated extensions, and to Hopf algebras, big Galois representations.