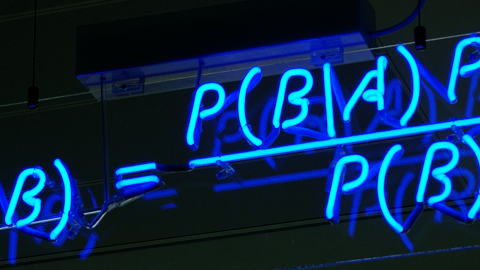About 10 years ago Minahan and Zarembo made a remarkable discovery: the one-loop Dilatation Operator in the SO(6) sector of planar N=4 SYM can be identified with the Hamiltonian of an integrable spin chain. This one-loop Dilatation operator was obtained by computing a two-point correlation function at one loop, which is a completely off-shell quantity. Around the same time, Witten proposed a duality between N=4 SYM and twistor string theory, which initiated a revolution in the field of on-shell objects like scattering amplitudes. In this talk we illustrate that these techniques that have been sucessfully used for on-shell quantities can also be employed for the computation of off-shell quantities by computing the one-loop Dilatation Operator in the SO(6) sector. The first half of the talk will be dedicated to doing this calculation using MHV diagrams and the second half of the talk shows the computation in twistor space. 

These two short talks will be followed by an informal afternoon session for those interested in further details of these approaches, and in form factors in Class Room C2 from 2-4.30 pm then from 4.30pm in N3.12.  All are welcome.

The cube attack of Dinur and Shamir and the AIDA attack of Vielhaber have been used successfully on 

reduced round versions of the Trivium stream cipher and a few other ciphers. 

These attacks can be viewed in the framework of higher order differentiation, as introduced by Lai in 

the cryptographic context. We generalise these attacks from the binary case to general finite fields, 

showing that we would need to differentiate several times with respect to each variable in order to have

a reasonable chance of a successful attack.

We also investigate the notion of “fast points” for a binary polynomial function f  

(i.e. vectors such that the derivative of f with respect to this vector has a lower 

than expected degree). These were  introduced by Duan and Lai, motivated by the fact that higher order 

differential attacks are usually more efficient if they use such points. The number of functions which 

admit fast points were computed by Duan et al in a few particular cases; we give explicit formulae for 

all remaining cases and discuss the cryptographic significance of these results.

This is joint work with Richard A. Davis (Columbia Statistics) and Johannes Heiny (Copenhagen). In recent years the sample covariance matrix of high-dimensional vectors with iid entries has attracted a lot of attention. A deep theory exists if the entries of the vectors are iid light-tailed; the Tracy-Widom distribution typically appears as weak limit of the largest eigenvalue of the sample covariance matrix. In the heavy-tailed case (assuming infinite 4th moments) the situation changes dramatically. Work by Soshnikov, Auffinger, Ben Arous and Peche shows that the largest eigenvalues are approximated by the points of a suitable nonhomogeneous Poisson process. We follows this line of research. First, we consider a p-dimensional time series with iid heavy-tailed entries where p is any power of the sample size n. The point process of the scaled eigenvalues of the sample covariance matrix converges weakly to a Poisson process. Next, we consider p-dimensional heavy-tailed time series with dependence through time and across the rows. In particular, we consider entries with a linear dependence or a stochastic volatility structure. In this case, the limiting point process is typically a Poisson cluster process. We discuss the suitability of the aforementioned models for large portfolios of return series. 

We describe the possible influence of stochastic 
dependence on the evaluation of
the risk of joint portfolios and establish relevant risk bounds.Some 
basic tools for this purpose are  the distributional transform,the 
rearrangement method and extensions of the classical Hoeffding -Frechet 
bounds based on duality theory.On the other hand these tools find also 
essential applications to various problems of optimal investments,to the 
construction of cost-efficient payoffs as well as to various optimal 
hedging problems.We
discuss in detail the case of optimal payoffs in Levy market models as 
well as utility optimal payoffs and hedgings
with state dependent utilities.