Homological Filling Functions
Abstract
I will discuss various types of filling functions on topological spaces, stating some results in the area. I will then go onto prove that a finitely presented subgroup of a hyperbolic group of cohomological dimension 2 is hyperbolic. On the way I will prove a stronger result about filling functions of subgroups of hyperbolic groups of cohomological dimension $n$.
Random walks and isoperimetric inequalities
Abstract
In this talk I will try to show how certain asymptotic properties of a random walk on a graph are related to geometric properties of the graph itself. A special focus will be put on spectral properties and isoperimetric inequalities, proving Kesten's criterion for amenability.
Bounds on Splittings of Groups
Abstract
We say a group is accessible if the process of iteratively decomposing G as an amalgamated free product or HNN extension over a finite group terminates in a finite number of steps. We will see Dunwoody's proof that FP2 groups are accessible, but that finitely generated groups need not be. If time permits, we will examine generalizations by Bestvina-Feighn, Sela and Louder.
Drones may evoke fear and possibility in equal measure, but they also are capable of giving us fresh perspectives, in this case a fascinating journey around the architecture and mathematics of the Andrew Wiles Building, from the unique Penrose tiling at the entrance to the building to the Crystal in the interior which floods light in to the lecture area below and whose shape represents the frequencies of a vibrating drum.
Thompson's Groups
Abstract
This talk will be an introduction to the weird and wonderful world of Thompson's groups $F$, $T$ and $V$. For example, the group $T$ was the first known finitely presented infinite simple group, $V$ has a finitely presented subgroup with co-NP-complete word problem, and whether or not $F$ is amenable is an infamous open problem.
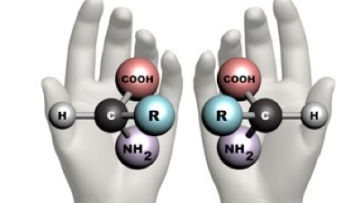
The word ‘chiral’ comes from the Greek word, kheir, which means ‘hand’. An object is said to be chiral if it cannot be superimposed on its mirror image. For instance, your hands are chiral. If you place your right hand over your left hand, it doesn’t fit – the thumbs stick out in opposite directions. And when you turn your hands to point them in the same direction the palm of your hand still looks different to the back of your hand.
A Survey of Results on the Section Conjecture
Abstract
After some generalities on étale fundamental groups and anabelian geometry, I will explore some of the current results on the section conjecture, including those of Koenigsmann and Pop on the birational section conjecture, and a recent unpublished result of Mohamed Saidi which reduces the section conjecture for finitely generated fields over the rationals to the case of number fields.
11:00