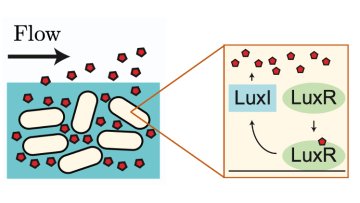
By pooling resources between cells, colonies of bacteria can exhibit behaviours far beyond the capabilities of an individual bacterium. For example, bacterial populations can encase themselves in a self-generated polymer matrix that shelters cells in the core of the population from the external environment. Such communities are termed “bacterial biofilms”, and show increased tolerance to antimicrobial treatments such as antibiotics.
14:30
Global Riemannian acceleration in hyperbolic and spherical spaces
Abstract
Riemannian optimization is a powerful and active area of research that studies the optimization of functions defined on manifolds with structure. A class of functions of interest is the set of geodesically convex functions, which are functions that are convex when restricted to every geodesic. In this talk, we will present an accelerated first-order method, nearly achieving the same rates as accelerated gradient descent in the Euclidean space, for the optimization of smooth and g-convex or strongly g-convex functions defined on the hyperbolic space or a subset of the sphere. We will talk about accelerated optimization of another non-convex problem, defined in the Euclidean space, that we solve as a proxy. Additionally, for any Riemannian manifold of bounded sectional curvature, we will present reductions from optimization methods for smooth and g-convex functions to methods for smooth and strongly g-convex functions and vice versa.
This talk is based on the paper https://arxiv.org/abs/2012.03618.
-
A link for this talk will be sent to our mailing list a day or two in advance. If you are not on the list and wish to be sent a link, please contact @email.
In the bleak, school-less midwinter, James Munro and his student crew have been keeping the maths going for high school students who want to step aside from the curriculum for an hour or so and peek round the corner at University Maths. Cue novels, (yes there is literature as well), dragons and your favourite graph.
On Set-valued Backward SDEs and Related Issues in Set-valued Stochastic Analysis
Abstract
Abstract: In this talk we try to establish an analytic framework for studying Set-Valued Backward Stochastic Differential Equations (SVBSDE for short), motivated largely by the current studies of dynamic set-valued risk measures for multi-asset or network-based financial models. Our framework will be based on the notion of Hukuhara difference between sets, in order to compensate the lack of “inverse” operation of the traditional Minkowski addition, whence the vector space structure, in traditional set-valued analysis. We shall examine and establish a useful foundation of set-valued stochastic analysis under this algebraic framework, including some fundamental issues regarding Aumann-Itˆo integrals, especially when it is connected to the martingale representation theorem. We shall identify some fundamental challenges and propose some extensions of the existing theory that are necessary to study the SVBSDEs. This talk is based on the joint works with C¸ a˘gın Ararat and Wenqian Wu.
Kinetic Theory for Hamilton-Jacobi PDEs
Abstract
The flow of a Hamilton-Jacobi PDE yields a dynamical system on the space of continuous functions. When the Hamiltonian function is convex in the momentum variable, and the spatial dimension is one, we may restrict the flow to piecewise smooth functions and give a kinetic description for the solution. We regard the locations of jump discontinuities of the first derivative of solutions as the sites of particles. These particles interact via collisions and coagulations. When these particles are selected randomly according to certain Gibbs measures initially, then the law of particles remains Gibbsian at later times, and one can derive a Boltzmann/Smoluchowski type PDE for the evolution of these Gibbs measures. In higher dimensions, we assume that the Hamiltonian function is independent of position and that the initial condition is piecewise linear and convex. Such initial conditions can be identified as (Laguerre) tessellations and the Hamilton-Jacobi evolution can be described as a billiard on the set of tessellations.
Risk-Taking Contest and its Mean Field Approximation
Abstract
Following the risk-taking model of Seel and Strack, n players decide when to stop privately observed Brownian motions with drift and absorption at zero. They are then ranked according to their level of stopping and paid a rank-dependent reward. We study the optimal reward design where a principal is interested in the average performance and the performance at a given rank. While the former can be related to reward inequality in the Lorenz sense, the latter can have a surprising shape. Next, I will present the mean-field version of this problem. A particular feature of this game is to be tractable without necessarily being smooth, which turns out to offer a cautionary tale. We show that the mean field equilibrium induces n-player ε-Nash equilibria for any continuous reward function— but not for discontinuous ones. We also analyze the quality of the mean field design (for maximizing the median performance) when used as a proxy for the optimizer in the n-player game. Surprisingly, the quality deteriorates dramatically as n grows. We explain this with an asymptotic singularity in the induced n-player equilibrium distributions. (Joint work with M. Nutz)
Oxford Mathematician Georgia Brennan has won a silver medal in the Mathematical Sciences category at STEM for Britain 2021 for her poster (extract in the image) on 'Mathematically Modelling Clearance in Alzheimer’s Disease: A Mathematical Drug Trial for the UK’s Protein Pandemic'.