The Oxford Mathematics educational experience is a journey, a journey like any other educational experience. It builds on what you learn at school. It is not unfamiliar and we don't want it to invisible. But it has aspects that are different. One of these is the tutorial system. Students have lectures. But they also have tutorials based on those lectures where they sit, usually in pairs, with a tutor, go through their work and, critically, get to ask questions. It is their tutorial.
Multispectral snapshot demosaicing via non-convex matrix completion
Abstract
Snapshot mosaic multispectral imagery acquires an undersampled data cube by acquiring a single spectral measurement per spatial pixel. Sensors which acquire p frequencies, therefore, suffer from severe 1/p undersampling of the full data cube. We show that the missing entries can be accurately imputed using non-convex techniques from sparse approximation and matrix completion initialised with traditional demosaicing algorithms.
Mechano-electrophysiological coupling in axonal membrane: theory, controversy and neuromodulation
Virtual fibring of manifolds and groups
Abstract
I will discuss Agol's proof of the Virtually Fibred Conjecture of
Thurston, focusing on the role played by the `RFRS' property. I will
then show how one can modify parts of Agol's proof by replacing some
topological considerations with a group theoretic statement about
virtual fibring of RFRS groups.
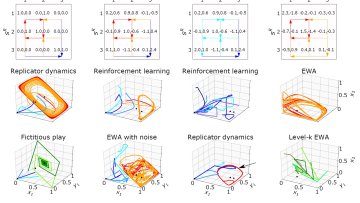
The concept of equilibrium is one of the most central ideas in economics. It is one of the core assumptions in the vast majority of economic models, including models used by policymakers on issues ranging from monetary policy to climate change, trade policy and the minimum wage. But is it a good assumption?
Developing the Next Generation of Image Reconstruction in Atom Probe Tomography
Abstract
Atom Probe Tomography is a powerful 3D mass spectrometry technique. By pulsing the sample apex with an electric field, surface atoms are ionised and collected by a detector. A 3D image of estimated initial ion positions is constructed via an image reconstruction protocol. Current protocols assume ion trajectories follow a stereographic projection. However, this method assumes a hemispherical sample apex that fails to account for varying material ionisation rates and introduces severe distortions into atomic distributions for complex material systems.
We aim to develop continuum models and use this to derive a time-dependent mapping describing how ion initial positions on the sample surface correspond to final impact positions on the detector. When correctly calibrated with experiment, such a mapping could be used for performing reconstruction.
Currently we track the sample surface using a level set method, while the electric field is solved via BEM or a FEM-BEM coupling. These field calculations must remain accurate close to the boundary. Calibrating unknown evaporation parameters with experiment requires an ensemble of models per experiment. Therefore, we are also looking to maximise model efficiency via BEM compression methods i.e. fast multipole BEM. Efficiently constructing and reliably interpolating the non-bijective trajectory mapping, while accounting for ion trajectory overlap and instabilities (at sample surface corners), also presents intriguing problems.
This project is in collaboration with Cameca, the leading manufacturer of commercial atom probe instruments. If successful in minimising distortions such a technique could become valuable within the semiconductor industry.
Oxford Mathematician Thomas Prince talks about his work on the construction of Fano manifolds in dimension four and their connection with Calabi-Yau geometry.
Dynamically consistent parameterization of mesoscale eddies
Abstract
This work aims at developing new approach for parameterizing mesoscale eddy effects for use in non-eddy-resolving ocean circulation models. These effects are often modelled as some diffusion process or a stochastic forcing, and the proposed approach is implicitly related to the latter category. The idea is to approximate transient eddy flux divergence in a simple way, to find its actual dynamical footprints by solving a simplified but dynamically relevant problem, and to relate the ensemble of footprints to the large-scale flow properties.
The strange instability of the equatorial Kelvin wave
Abstract
The Kelvin wave is perhaps the most important of the equatorially trapped waves in the terrestrial atmosphere and ocean, and plays a role in various phenomena such as tropical convection and El Nino. Theoretically, it can be understood from the linear dynamics of a stratified fluid on an equatorial beta plane, which, with simple assumptions about the disturbance structure, leads to wavelike solutions propagating along the equator, with exponential decay in latitude. However, when the simplest possible background flow is added (with uniform latitudinal shear), the Kelvin wave (but not the other equatorial waves) becomes unstable. This happens in an extremely unusual way: there is instability for arbitrarily small nondimensional shear p, and the growth rate is proportional to exp(-1/p^2) as p->0. This in contrast to most hydrodynamic instabilities, in which the growth rate typically scales as a positive power of p-p_c as the control parameter p passes through a critical value p_c.
This Kelvin wave instability has been established numerically by Natarov and Boyd, who also speculated as to the underlying mathematical cause. Here we show how the growth rate and full spatial structure of the instability may be derived using matched asymptotic expansions applied to the (linear) equations of motion. This involves an adventure with Whittaker functions in the exponentially-decaying tails of the Kelvin waves, and a trick to reveal the exponentially small growth rate from a formulation that only uses regular perturbation expansions. Numerical verification of the analysis is also interesting and challenging, since special high-precision solutions of the governing ODE are required even when the nondimensional shear is not that small (circa 0.5).