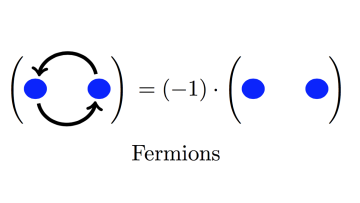
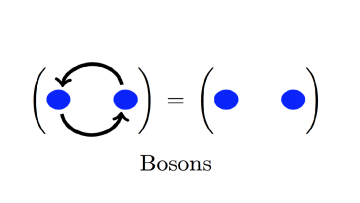
Elementary particles in two dimensional systems are not constrained by the fermion-boson alternative. They are so-called "anyons''. Anyon systems are modelled by modular tensor categories, and form an active area of research. Oxford Mathematician André Henriques explains his interest in the question.
Axiomatizability and profinite groups
Abstract
A mathematical structure is `axiomatizable' if it is completely determined by some family of sentences in a suitable first-order language. This idea has been explored for various kinds of structure, but I will concentrate on groups. There are some general results (not many) about which groups are or are not axiomatizable; recently there has been some interest in the sharper concept of 'finitely axiomatizable' or FA - that is, when only a finite set of sentences (equivalently, a single sentence) is allowed.
While an infinite group cannot be FA, every finite group is so, obviously. A profinite group is kind of in between: it is infinite (indeed, uncountable), but compact as a topological group; and these groups share many properties of finite groups, though sometimes for rather subtle reasons. I will discuss some recent work with Andre Nies and Katrin Tent where we prove that certain kinds of profinite group are FA among profinite groups. The methods involve a little model theory, and quite a lot of group theory.