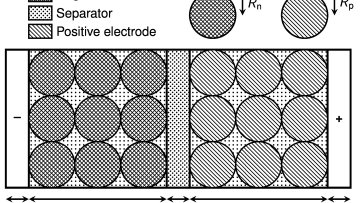
Have you ever wished that the battery on your phone would last longer? That you could charge it up more rapidly? Maybe you have thought about buying an electric vehicle, but were filled with range anxiety – the overwhelming fear that the battery will run out before you reach your destination, leaving you stranded? Oxford Mathematicians are hard at work demonstrating that mathematics may provide the key to help tackle problems faced by the battery industry.
What is Arakelov Geometry?
Abstract
Arakelov geometry studies schemes X over ℤ, together with the Hermitian complex geometry of X(ℂ).
Most notably, it has been used to give a proof of Mordell's conjecture (Faltings's Theorem) by Paul Vojta; curves of genus greater than 1 have at most finitely many rational points.
In this talk, we'll introduce some of the ideas behind Arakelov theory, and show how many results in Arakelov theory are analogous—with additional structure—to classic results such as intersection theory and Riemann Roch.
Cartier Operators
Abstract
Given a morphism of schemes of characteristic p, we can construct a morphism from the exterior algebra of Kahler differentials to the cohomology of De Rham complex, which is an isomorphism when the original morphism is smooth.
Hölder regularity for nonlocal double phase equations
Abstract
We present some regularity estimates for viscosity solutions to a class of possible degenerate and singular integro-differential equations whose leading operator switches between two different types of fractional elliptic phases, according to the zero set of a modulating coefficient a = a(·, ·). The model case is driven by the following nonlocal double phase operator,
$$\int \frac{|u(x) − u(y)|^{p−2} (u(x) − u(y))} {|x − y|^{n+sp}} dy+ \int a(x, y) \frac{|u(x) − u(y)|^{ q−2} (u(x) − u(y))} {|x − y|^{n+tq}} dy$$
where $q ≥ p$ and $a(·, ·) = 0$. Our results do also apply for inhomogeneous equations, for very general classes of measurable kernels. By simply assuming the boundedness of the modulating coefficient, we are able to prove that the solutions are Hölder continuous, whereas similar sharp results for the classical local case do require a to be Hölder continuous. To our knowledge, this is the first (regularity) result for nonlocal double phase problems.
Financial modelling and utilisation of a diverse range of data sets in oil markets
Abstract
We will present three problems that we are interested in:
Forecast of volatility both at the instrument and portfolio level by combining a model based approach with data driven research
We will deal with additional complications that arise in case of instruments that are highly correlated and/or with low volumes and open interest.
Test if volatility forecast improves metrics or can be used to derive alpha in our trading book.
Price predication using physical oil grades data
Hypothesis:
Physical markets are most reflective of true fundamentals. Derivative markets can deviate from fundamentals (and hence physical markets) over short term time horizons but eventually converge back. These dislocations would represent potential trading opportunities.
The problem:
Can we use the rich data from the physical market prices to predict price changes in the derivative markets?
Solution would explore lead/lag relationships amongst a dataset of highly correlated features. Also explore feature interdependencies and non-linearities.
The prediction could be in the form of a price target for the derivative (‘fair value’), a simple direction without magnitude, or a probabilistic range of outcomes.
Modelling oil balances by satellite data
The flow of oil around the world from being extracted, refined, transported and consumed, forms a very large dynamic network. At both regular and irregular intervals, we can make noisy measurements of the amount of oil at certain points in the network.
In addition, we have general macro-economic information about the supply and demand of oil in certain regions.
Based on that information, with general information about the connections between nodes in the network i.e. the typical rate of transfer, one can build a general model for how oil flows through the network.
We would like to build a probabilistic model on the network, representing our belief about the amount of oil stored at each of our nodes, which we refer to as balances.
We want to focus on particular parts of the network where our beliefs can be augmented by satellite data, which can be done by focusing on a sub network containing nodes that satellite measurements can be applied to.
Complete Complexes and Spectral Sequences (COW Seminar)
Abstract
The space of complete collineations is an important and beautiful chapter of algebraic geometry, which has its origins in the classical works of Chasles, Schubert and many others, dating back to the 19th century. It provides a 'wonderful compactification' (i.e. smooth with normal crossings boundary) of the space of full-rank maps between two (fixed) vector spaces. More recently, the space of complete collineations has been studied intensively and has been used to derive groundbreaking results in diverse areas of mathematics. One such striking example is L. Lafforgue's compactification of the stack of Drinfeld's shtukas, which he subsequently used to prove the Langlands correspondence for the general linear group.
In joint work with M. Kapranov, we look at these classical spaces from a modern perspective: a complete collineation is simply a spectral sequence of two-term complexes of vector spaces. We develop a theory involving more full-fledged (simply graded) spectral sequences with arbitrarily many terms. We prove that the set of such spectral sequences has the structure of a smooth projective variety, the 'variety of complete complexes', which provides a desingularization, with normal crossings boundary, of the 'Buchsbaum-Eisenbud variety of complexes', i.e. a 'wonderful compactification' of the union of its maximal strata.
Classifying Fine Compactified Universal Jacobians (COW seminar)
Abstract
A fine compactified Jacobian is a proper open substack of the moduli space of simple sheaves. We will see that fine compactified Jacobians correspond to a certain combinatorial datum, essentially obtained by taking multidegrees of all elements of the compactified Jacobian. This picture generalizes to flat families of curves. We will discuss a classification result in the case when the family is the universal family over the moduli space of curves. This is a joint work with Jesse Kass.
Simplicity of Tannakian Categories (COW Seminar)
Abstract
Let A be a Tannakian category. Any exact tensor functor defined on A is either zero, or faithful. In this talk, I want to draw attention to a derived analogue of this statement (in characteristic zero) due to Jack Hall and David Rydh, and discuss some remarkable consequences for certain classification problems in algebraic geometry.
This autumn we welcomed the first students on the EPSRC CDT in Mathematics of Random Systems: Analysis, Modelling and Algorithms. The CDT (Centre for Doctoral Training) is a partnership between the Mathematical Institute and the Department of Statistics here in Oxford, and the Department of Mathematics, Imperial College London. Its ambition is to train the next generation of academic and industry experts in stochastic modelling, advanced computational methods and Data Science.