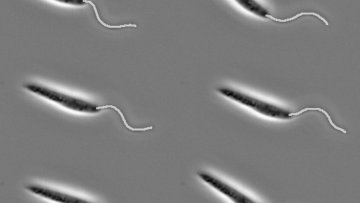
Oxford Mathematician Benjamin Walker talks about his work on the automatic identification of flagella from images, opening up a world of data-driven analysis.
Hyperbolic hydrodynamic limit of a anharmonic chain under boundary tension
Abstract
"We study the hydrodynamic limit for the isothermal dynamics of an anharmonic chain under hyperbolic space-time scaling under varying tension. The temperature is kept constant by a contact with a heat bath, realised via a stochastic momentum-preserving noise added to the dynamics. The noise is designed to be large at the microscopic level, but vanishing in the macroscopic scale. Boundary conditions are also considered: one end of the chain is kept fixed, while a time-varying tension is applied to the other end. We show that the volume stretch and momentum converge to a weak solution of the isothermal Euler equations in Lagrangian coordinates with boundary conditions."
16:00
The mechanics and mathematics of bodies described by implicit constitutive equations
Abstract
After discussing the need for implicit constitutive relations to describe the response of both solids and fluids, I will discuss applications wherein such implicit constitutive relations can be gainfully exploited. It will be shown that such implicit relations can explain phenomena that have hitherto defied adequate explanation such as fracture and the movement of cracks in solids, the response of biological matter, and provide a new way to look at numerous non-linear phenomena exhibited by fluids. They provide a totally new and innovative way to look at the problem of Turbulence. It also turns out that classical Cauchy and Green elasticity are a small subset of the more general theory of elastic bodies defined by implicit constitutive equations.
16:00
On the Type I blow-up for the incompressible Euler equations
Abstract
In this talk we discuss the Type I blow up and the related problems in the 3D Euler equations. We say a solution $v$ to the Euler equations satisfies Type I condition at possible blow up time $T_*$ if $\lim\sup_{t\nearrow T_*} (T_*-t) \|\nabla v(t)\|_{L^\infty} <+\infty$. The scenario of Type I blow up is a natural generalization of the self-similar(or discretely self-similar) blow up. We present some recent progresses of our study regarding this. We first localize previous result that ``small Type I blow up'' is absent. After that we show that the atomic concentration of energy is excluded under the Type I condition. This result, in particular, solves the problem of removing discretely self-similar blow up in the energy conserving scale, since one point energy concentration is necessarily accompanied with such blow up. We also localize the Beale-Kato-Majda type blow up criterion. Using similar local blow up criterion for the 2D Boussinesq equations, we can show that Type I and some of Type II blow up in a region off the axis can be excluded in the axisymmetric Euler equations. These are joint works with J. Wolf.
16:00
Measuring families of curves
Abstract
For measuring families of curves, or, more generally, of measures, $M_p$-modulus is traditionally used. More recent studies use so-called plans on measures. In their fundamental paper Ambrosio, Di Marino and Savare proved that these two approaches are in some sense equivalent within $1<p<\infty$. We consider the limiting case $p=1$ and show that the $AM$-modulus can be obtained alternatively by the plan approach. On the way, we demonstrate unexpected behavior of the $AM$-modulus in comparison with usual capacities.
This is a joint work with Vendula Honzlov\'a Exnerov\'a, Ond\v{r}ej F.K. Kalenda and Olli Martio. Partially supported by the grant GA\,\v{C}R P201/18-07996S of the Czech Science Foundation.
Remarks on Euler equations
Abstract
I'll talk about smooth solutions of Euler equations with compactly supported velocities, and applications to other equations.
Self-dual cuspidal and supercuspidal representations
Abstract
According to the Harish-Chandra philosophy, cuspidal representations are the basic building blocks in the representation theory of finite reductive groups. Similarly for supercuspidal representations of p-adic groups. Self-dual representations play a special role in the study of parabolic induction. Thus, it is of interest to know whether self-dual (super)cuspidal representations exist. With a few exceptions involving some small fields, I will show precisely when a finite reductive group has irreducible cuspidal representations that are self-dual, of Deligne-Lusztig type, or both. Then I will look at implications for the existence of irreducible, self-dual supercuspidal representations of p-adic groups. This is joint work with Manish Mishra.
If you are Interested in postgraduate study and curious about what it would be like to do research at Oxford we are delighted to announce that Oxford Mathematics is taking part in the UNIQ+ pilot programme, a six-week summer school encouraging access to postgraduate study from under-represented groups in UK universities.
Segre-Driven Ideal Membership Testing
Abstract
In this talk we discuss new effective methods to test pairwise containment of arbitrary (possibly singular) subvarieties of any smooth projective toric variety and to determine algebraic multiplicity without working in local rings. These methods may be implemented without using Gröbner bases; in particular any algorithm to compute the number of solutions of a zero-dimensional polynomial system may be used. The methods arise from techniques developed to compute the Segre class s(X,Y) of X in Y for X and Y arbitrary subschemes of some smooth projective toric variety T. In particular, this work also gives an explicit method to compute these Segre classes and other associated objects such as the Fulton-MacPherson intersection product of projective varieties.
These algorithms are implemented in Macaulay2 and have been found to be effective on a variety of examples. This is joint work with Corey Harris (University of Oslo).