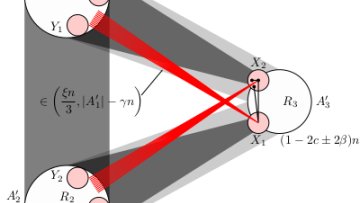
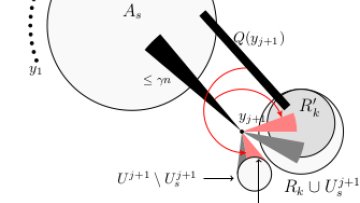
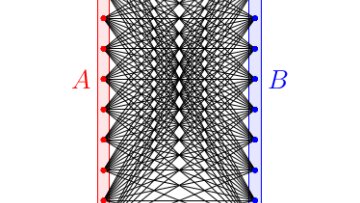
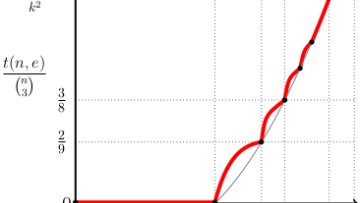
Oxford Mathematician Katherine Staden provides a fascinating snapshot of the field of combinatorics, and in particular extremal combinatorics, and the progress that she and her collaborators are making in answering one of its central questions posed by Paul Erdős over sixty years ago.
Regularity vs. singularity for elliptic and parabolic systems
Abstract
Hilbert's 19th problem asks if minimizers of "natural" variational integrals are smooth. For the past century, this problem inspired fundamental regularity results for elliptic and parabolic PDES. It also led to the construction of several beautiful counterexamples to regularity. The dichotomy of regularity vs. singularity is related to that of single PDE (the scalar case) vs. system of PDEs (the vectorial case), and low dimension vs. high dimension. I will discuss some interesting recent counterexamples to regularity in low-dimensional vectorial cases, and outstanding open problems. Parts of this are joint works with A. Figalli and O. Savin.
14:30
More Designs
Abstract
We generalise the existence of combinatorial designs to the setting of subset sums in lattices with coordinates indexed by labelled faces of simplicial complexes. This general framework includes the problem of decomposing hypergraphs with extra edge data, such as colours and orders, and so incorporates a wide range of variations on the basic design problem, notably Baranyai-type generalisations, such as resolvable hypergraph designs, large sets of hypergraph designs and decompositions of designs by designs. Our method also gives approximate counting results, which is new for many structures whose existence was previously known, such as high dimensional permutations or Sudoku squares.
Effective Mathematics: a disruptive technology in the era of the cloud
Abstract
Lincoln Wallen is the Former CTO, Dreamworks Animation. All are welcome