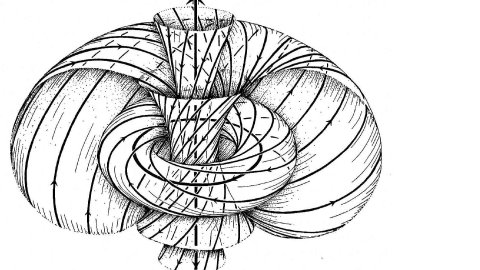
Doubled Geometry and $\alpha'$ Corrections
Abstract
I review work done in collaboration with Siegel and Zwiebach, in which a doubled geometry is developed that provides a spacetime action containing the standard gravity theory for graviton, Kalb-Ramond field and dilaton plus higher-derivative corrections. In this framework the T-duality O(d,d) invariance is manifest and exact to all orders in $\alpha'$. This theory by itself does not correspond to a standard string theory, but it does encode the Green-Schwarz deformation characteristic of heterotic string theory to first order in $\alpha'$ and a Riemann-cube correction to second order in $\alpha'$. I outline how this theory may be extended to include arbitrary string theories.
16:00
Inverse limits of upper semicontinuous functions and indecomposable continua
How can we explain the patterns of genetic variation in the world around us? The genetic composition of a population can be changed by natural selection, mutation, mating, and other genetic, ecological and evolutionary mechanisms. How do they interact with one another, and what was their relative importance in shaping the patterns we see today?
A multilevel method for semidefinite programming relaxations of polynomial optimization problems with structured sparsity
Abstract
We propose a multilevel paradigm for the global optimisation of polynomials with sparse support. Such polynomials arise through the discretisation of PDEs, optimal control problems and in global optimization applications in general. We construct projection operators to relate the primal and dual variables of the SDP relaxation between lower and higher levels in the hierarchy, and theoretical results are proven to confirm their usefulness. Numerical results are presented for polynomial problems that show how these operators can be used in a hierarchical fashion to solve large scale problems with high accuracy.
Second order approximation of the MRI signal for single shot parameter assessment
Abstract
Most current methods of Magnetic Resonance Imaging (MRI) reconstruction interpret raw signal values as samples of the Fourier transform of the object. Although this is computationally convenient, it neglects relaxation and off–resonance evolution in phase, both of which can occur to significant extent during a typical MRI signal. A more accurate model, known as Parameter Assessment by Recovery from Signal Encoding (PARSE), takes the time evolution of the signal into consideration. This model uses three parameters that depend on tissue properties: transverse magnetization, signal decay rate, and frequency offset from resonance. Two difficulties in recovering an image using this model are the low SNR for long acquisition times in single-shot MRI, and the nonlinear dependence of the signal on the decay rate and frequency offset. In this talk, we address the latter issue by using a second order approximation of the original PARSE model. The linearized model can be solved using convex optimization augmented with well-stablished regularization techniques such as total variation. The sensitivity of the parameters to noise and computational challenges associated with this approximation will be discussed.
The motion of weights attached to a chain or string moving on a frictionless pulley is a classic problem of introductory physics used to understand the relationship between force and acceleration. In their recently published paper Oxford Mathematicians Dominic Vella and Alain Goriely and colleagues looked at the dynamics of the chain when one of the weights is removed and thus one end is pulled with constant acceleration.
(COW SEMINAR) Monodromy and derived equivalences
Abstract
This is will be a progress report on our long-ongoing joint work with Bezrukavnikov on lifting the monodromy of the quantum differential equation for symplectic resolutions to automorphisms of their derived categories of coherent sheaves. I will attempt to define the ingredient that go both into the problem and into its solution.
(COW SEMINAR) Higgs bundles and determinant divisors
Abstract
Following an idea of Gaiotto, a symplectic representation of a complex Lie group G defines a complex Lagrangian subvariety inside the moduli space of G-Higgs bundles. The talk will discuss the case of G=SL(2) and its link with determinant divisors, or equivalently Brill-Noether loci, in the moduli space of semistable SL(2)-bundles.