L is for Logic

Brian Tyrrell
Postgraduate Student in Mathematics
 

Brian Tyrrell is a DPhil student, part of the Logic research group. He tends to think about geometric versions of Hilbert's Tenth Problem, and more generally about undecidability found across number theory and algebraic geometry. In his spare time he likes to prove things - primarily sourdough boules.

Entry about Model Theory in the Stanford Encyclopedia of Philosophy by Wilfrid Hodges. 

Marcus du Sautoy discusses Gödel's Incompleteness Theorem on Numberphile. 

Magic: The Gathering (popular trading card combat game) is Turing complete. Based on this paper by Churchill et al. 

Gödel, Escher, Bach: an Eternal Golden Braid, by Douglas Hofstadter. Pulitzer Prize-winning book on a range of topics in mathematics and philosophy. 

TED talk on Hilbert’s Paradox of the Grand Hotel; a thought experiment on infinite sets. 

Wikipedia page on the Topologist’s Sine Curve, an example of “pathological behaviour” that arises in analysis but not in o-minimality. 

Download the A3 poster as a pdf

Logic is a vast and ancient field, and its influence spans not only mathematics but philosophy, computer science, and linguistics. Even in mathematics one cannot pin down exactly where “logic” as a subject lies – it appears as set theory, computability theory, model theory, and proof theory. Since the work of Gottlob Frege and Bertrand Russell in the 19th century, however, mathematical logic has been used as a foundational language underpinning all mathematical discussion.  

In the Oxford Mathematical Institute, logicians mainly research in model theory, a branch of logic which studies the connection between mathematical semantics (truth) and mathematical syntax (proof). A core result in this field tells one that in first-order logic there is an absolute correspondence between semantics and syntax: if a statement is logically valid (“true”), it must be provable, and if a statement is provable, it must be true. First-order logic is built from finite application of connectives \(\wedge \) (and), \( \vee \) (or), \(\neg \) (not), and quantifiers \(\forall \) (for all), \(\exists \) (there exists), to a prescribed language of variables, constants, functions, and relations. 

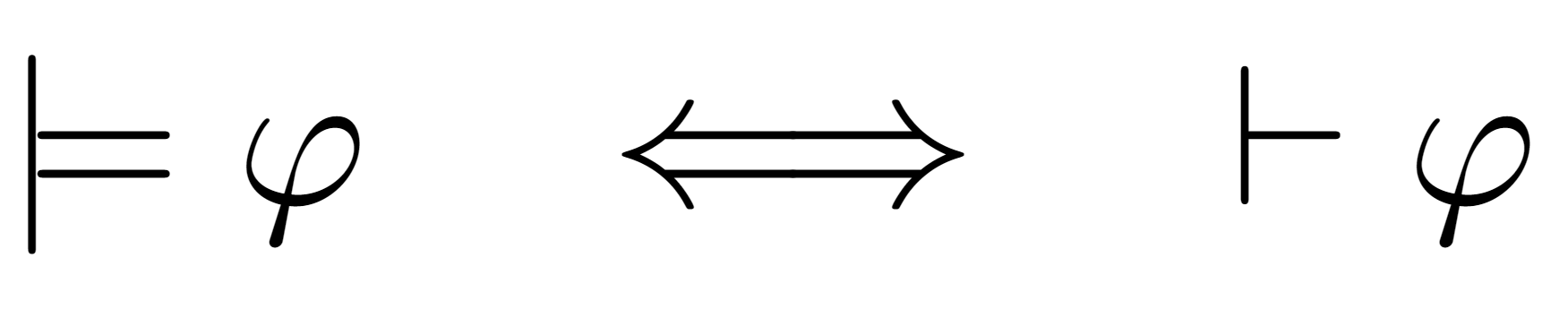
Illustration of the Completeness & Soundness Theorems, which prove a correspondence between semantic truth of a first-order sentence 𝜑 (left) and the existence of a proof of 𝜑 within first-order logic (right).

Logicians are interested in which subsets of a structure (such as a field, ordered group, polynomial ring) are definable, meaning that they can be described by a first-order formula.  Examples of definable subsets include, in arithmetic, the prime numbers; in any group, its centraliser and abelianization; or in \( \mathbb{ℚ}\) (the set of rational numbers), the set \(\mathbb{Z}\) of integers (though this is harder to prove!). Pure model theory has largely been shaped by Michael Morley, and later Saharon Shelah, and aims to classify structures by what can and cannot be defined (or even “interpreted”) in them.  

Applications of model theory are rife in combinatorics, algebra, number theory and geometry (among other fields). For example, in 1983 the geometer Gerd Faltings solved the Mordell Conjecture in proving that a curve over \( \mathbb{ℚ}\) has finitely many rational points when an associated invariant called its “genus” is 2 or more. Around this time Oxford Mathematicians Boris Zilber and Ehud Hrushovski developed geometric stability theory (a branch of model theory focused on geometric structures and dimensional notions therein), and the latter used this to solve the “geometric” Mordell-Lang Conjecture in 1996: an analogue of Faltings’ result in the positive characteristic function field setting, e.g. the algebraic closure of \( \mathbb{F_p(t)} \).

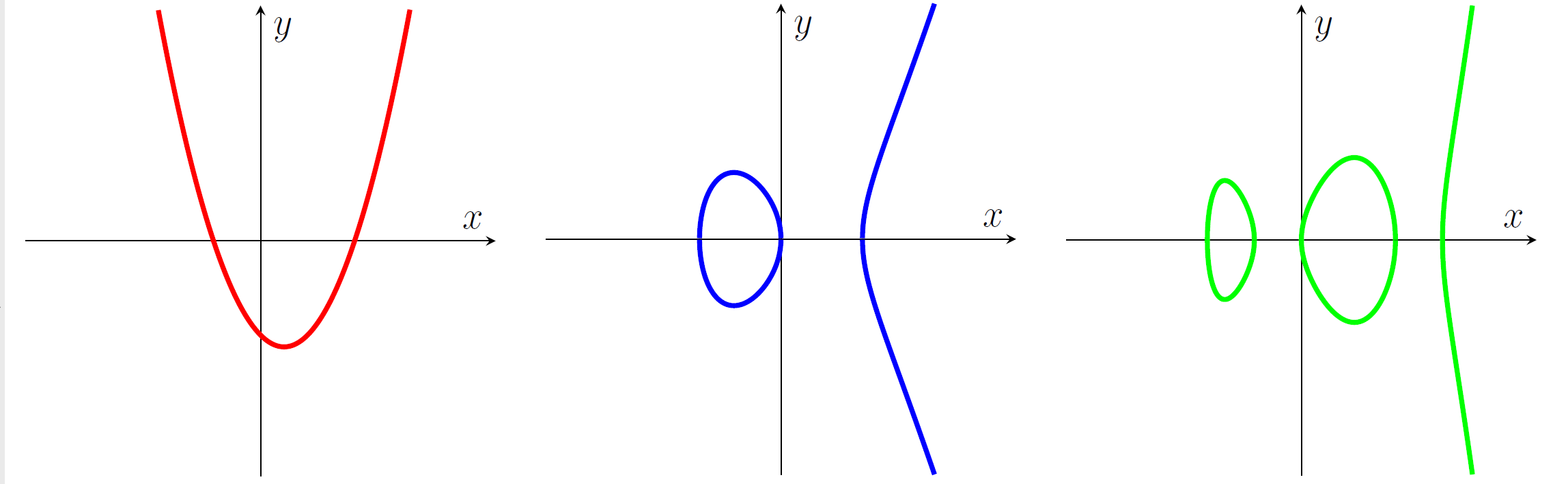
Left: \( y=x^2−x−2 \), curve of genus 0. Middle:  \(y^2=x^3−3x\), curve of genus 1.
Right: \(4y^2=x^5−2x^4−7x^3+8x^2+12x\), curve of genus 2.

One contribution of model theory to number theory is work on the André-Oort Conjecture (a proof of which Oxford Mathematician Jonathan Pila and collaborators Ananth Shankar, Jacob Tsimmerman, Hélène Esnault, and Michael Groechenig, announced in 2021). Pila attacked this problem using o-minimality, a subfield of model theory which arose from Alfred Tarski’s work on understanding the semialgebraic subsets of real space. It turns out these sets are exactly the ones definable in \( \mathbb{R}^n \) in the language {\(0\), \(1\), \(+\), \(×\), \(<\), \(=\)}. In particular, the definable subsets of \( \mathbb{R} \) are finite unions of points and intervals, making \( \mathbb{R} \) o-minimal by definition. Many results in real algebraic geometry thus have parallels in general o-minimal structures, and can be used to tackle Diophantine problems. In addition, o-minimal structures are so nice and versatile that they have been suggested as a better framework in which to develop topology, as they avoid certain analysis-based pathological behaviour.  

Alfred Tarski in Berkeley.

One result of Tarski’s exploration was the conclusion that first-order questions about ℝ as an ordered ring can be answered algorithmically – the structure is decidable. This contrasts with (for example) the existential questions about \(\mathbb{Z} \) as a ring. A result of Martin Davis, Hilary Putnam, Julia Robinson, and Yuri Matiyasevich shows that no computer program can ever exist that, upon the input of a polynomial \(f(x_1,…,x_n)∈ \mathbb{Z}[x_1,…,x_n]\), answers correctly when asked “do there exist \(x_1,…,x_n∈ \mathbb{Z} \) such that \(f(x_1,…,x_n) =0\)?”. This problem is mathematically undecidable. Oxford Mathematician Jochen Koenigsmann has contributed to the analogous problem of existential questions about \( \mathbb{ℚ} \) by showing that the non-integer rational numbers exactly satisfy a Diophantine equation (see D is for Diophantine Equations) over \( \mathbb{ℚ} \). This allows us to reduce some questions of the form “\( \forall x_1, ..., \forall x_n\) \(\exists y_1, ..., \exists y_m …\)” about \( \mathbb{ℚ} \) to existential questions about \( \mathbb{Z} \), which we know are undecidable. The decidability of existential questions about \( \mathbb{ℚ} \) is one of the many big unsolved problems of logic today – and the more logicians there are, the closer we will get to an answer!