Episode 10

In episode 10, Flora shows us a trick with a Möbius strip that you can try at home.

Topology

Wikipedia has a rigorous definition of a homeomorphism if you’re interested; a function between two topological spaces is a homeomorphism is it’s a bijection , it is continuous, and if the inverse function is also continuous.

Definitions have a special role in mathematics; anything that satisfies the definition is a homeomorphism, and anything that doesn’t satisfy the definition is not a homeomorphism. In practice that means that all questions of the form “are X and Y homeomorphic?” mean “is there a function f from X to Y that satisfies the definition of a homeomorphism?”, and it comes down to checking the conditions above. Some simple operations, like stretching, satisfy the definition, and working on topology involves building a toolkit of other homeomorphisms that we can use to show that two spaces are homeomorphic.

Flora also worked with “equivalence relations” to glue points together. Guess what, equivalence relations also have a rigorous definition! An equivalence relation is a binary relation (a new definition for things being "equal") which is reflexive ($x=x$ for all $x$), symmetric (if $x=y$ then $y=x$), and transitive (if $x=y$ and $y=z$ then $x=z$). Modular arithmetic, which we talked about last week, is an example of an equivalence relation.

Finally, here’s a link to the Wikipedia page on Quotient Spaces in Topology. This is the rigorous version of the “gluing” process that Flora described. This page is very technical (there’s a reason why this is second-year university mathematics!), but it has another good animation that’s worth having a look at.

Möbius Strips

Plus magazine reminds you of the suggested homework: make a Möbius strip yourself and cut along the halfway line, the 1/3 along line, etc. It also has an extra fun suggestion at the end!

When you’ve had a go at that, you could watch this; Topology & Geometry - Dr Tadashi Tokieda. This is a great lecture explaining what happens when you cut a Möbius strip along the halfway line, and again, and along the 1/3 along line, and why!

Random Graphs

Here’s a tidy version of the random graphs question that James mentioned;

Suppose four towns are connected by a road network; each pair of towns is connected by a road, and none of the roads connect with each other except at the towns. Each road is open for traffic with probability $p$ and closed with probability $1-p$, and each road is independent of the other roads. What’s the probability that I can drive from every town to every other town (not necessarily directly!)?

Four towns, with each pair linked by a road.

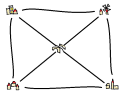
For example, if only the three roads from the town in the South-East are open, then I can still get from every town to every other town (via the town in the South-East). If all the roads are closed, then I definitely can’t get between any pair of towns. On the livestream, I suggested working case by case in terms of how many roads are open.

If you’ve got that probability in terms of $p$, you might like to try plotting it as a function of $p$. Next, you could repeat the whole calculation for five towns, or for six towns. What happens to the graph?

There’s more information about this problem for a large number of towns, and a link to a 1960 research paper, here.

Curve sketching

$$y=x^6+6x^5(1-x)+15x^4(1-x)^2+16x^3(1-x)^3, \quad \text{for}\quad 0\leq x \leq 1$$

This is a tricky polynomial to sketch. It’s got a factor of $x^3$, which might give you a clue about what it looks like near $x=0$. If you know the chain rule and the product rule and you’re feeling brave, you could try differentiating this and checking what’s going on at $x=1$.

Teddy Rocks Maths Essay Competition

This essay competition is open to anyone, and you can write about any mathematical topic you like. There are two £50 prizes (one of them is just for people aged $\leq 18$). Entries close 26 March at https://www.seh.ox.ac.uk/study/outreach/teddy-rocks-maths

If you want to get in touch with us about any of the mathematics in the video or the further reading, feel free to email us on oomc [at] maths.ox.ac.uk.