Season 2 Episode 12

In the last episode of Season 2, there are just a few more things to cover...

Further Reading

Chaos

There are many YouTube videos about chaos (which is why I had to pick a weird example, so that you wouldn’t immediately know where I was going with this)

• The Mandelbrot Set – Numberphile
• Chaos Game – Numberphile
• The Feigenbaum Constant (4.669) – Numberphile
• This equation will change how you see the world (the logistic map) – Veritasium
• Chaos: The Science of the Butterfly Effect – Veritasium

The obvious popular mathematics book to mention here is Chaos by James Gleick.

If you don’t want to watch the videos above, and you’d rather explore for yourself, then either use your calculator or a computer to investigate what happens if you iterate the function
\begin{equation*}
x_{n+1}=ax_n(1-x_n)
\end{equation*}
for different numbers $a$ between $1$ and $4$, and for different starting numbers $x_0$ between $0$ and $1$.

Tilings

I sped through the $3\times n$ calculation and I didn’t even get to the end, so here it is again.

Let’s write $a_n$ for the number of ways to tile a $3\times n$ board with dominoes, and write $b_n$ for the number of ways to tile a $3\times n$ board-with-one-corner-missing. By considering the different possibilities for how the left-hand edge is tiled;

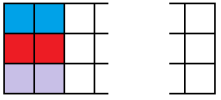
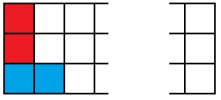
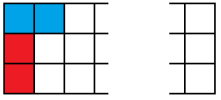
we find three different cases for the left edge. In each case, we’ve got a bit of tiling left to do, and we can write the number of ways to do that tiling in terms of $b_{n-1}$ and $a_{n-2}$.

We have $a_{n}=a_{n-2}+b_{n-1}+b_{n-1}$ for all $n\geq 2$.

We also need to consider how to tile a $3\times n$ board-with-one-corner missing. There are a couple of cases for how the left edge where the corner is missing might be tiled;

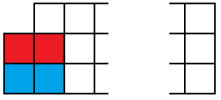
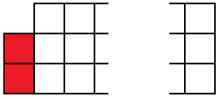
So we have $b_n=b_{n-2}+a_{n-1}$ for all $n\geq 2$.

Now we’ve got two recurrence relations to solve at once – that’s pretty tricky! We can make progress by substituting the first one into the second. The first one says that $2b_{n-1}=a_n-a_{n-2}$ for all $n\geq 2$. That’s the same thing as saying that $b_n=\frac{1}{2} (a_{n+1}-a_{n-1})$ for all $n\geq 1$ or $b_{n-2}=\frac{1}{2}(a_{n-1}-a_{n-3})$ for all $n\geq 3$.

So for $n\geq 3$, we can substitute these expressions into the second recurrence relation to get
$\frac{1}{2} (a_{n+1}-a_{n-1})=\frac{1}{2}(a_{n-1}-a_{n-3})+a_{n-1}$ for $n\geq 3$.

That rearranges to $a_{n+1}-4a_{n-1}+a_{n-3}$ for $n\geq 3$. We can use this recurrence relation to quickly generate the number of ways to tile a $3\times n$ board from smaller boards.

In fact, you learn at some point (possibly at university) that there’s a general solution to equations like that – the trick is to try $a_n= A x^n + B y^n$ where $A$ and $B$ and $x$ and $y$ are real numbers that you try to solve for, usually by trying $a_n=x^n$ first and finding any solutions (values for $x$ and $y$), and then choosing $A$ and $B$ to make sure that some small cases work.

L-shaped triominos

There’s a lovely problem to do with L-shaped triominos (that just means three squares arranged into an L-shape). It’s a little bit famous, but you might not have seen it, so here goes!

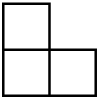
Step 1 – can you fit together four L-shaped triominos to make a larger L-shaped triomino?

Step 2 – if one corner is removed from an $8\times 8$ grid, can you cover the other 63 squares with 21 L-shaped triominos (each one lined up with three squares, no overlapping, no cutting up the pieces)?

Step 3 – what if a different square is removed from the chessboard – can you cover the other 63 squares with 21 L-shaped triominos?

Curve sketching

I think I might be almost out of interesting curves to sketch! There are ones that usually turn up in lists online like

$$y=x^x$$

but that's pretty hard to approach with AS-level Maths.

I suppose the only combination of $\sin x$ and $e^x$ that I haven't given you yet is

$$y=e^{e^x}$$

That function is part of my favourite integration question - find $\int e^{x+e^x}\,\mathrm{d}x$. No hints, but I'll link to this OOMC episode here and this one here.

If you want to get in touch with us about any of the mathematics in the video or the further reading, feel free to email us on oomc [at] maths.ox.ac.uk.