Geometry Solutions
Part of the Oxford MAT Livestream.
Revision Questions
1. Something like
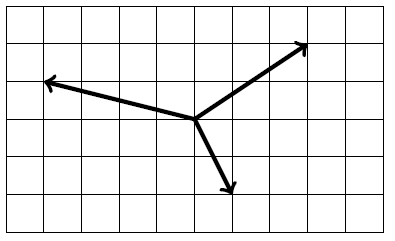
2. We add the components separately, so $\displaystyle \binom{3}{2}+\binom{-4}{1}=\binom{-1}{3}$.
My diagram now looks like this.
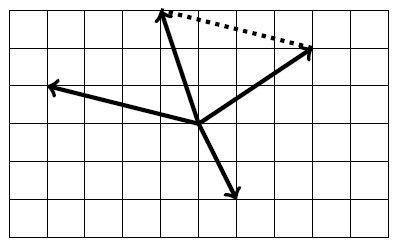
3. You multiply a vector by a scalar by multiplying each component, so $\displaystyle 3 \binom{-4}{1}=\binom{-12}{3}$ and $\displaystyle 2\binom{1}{-2}=\binom{2}{-4}$. Then add them together $\displaystyle \binom{-12}{3}+\binom{2}{-4}=\binom{-10}{-1}$.
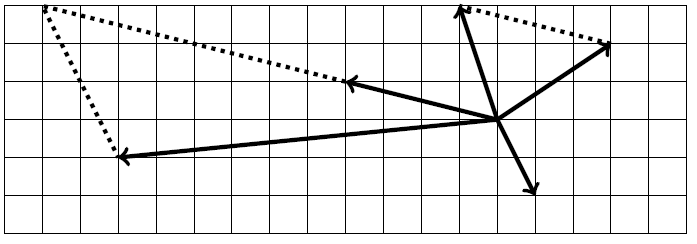
My diagram now looks like this.
4. This line has gradient $(-1-5)/(3-1)=-3$ and goes through $(1,5)$ so it's $y-5=-3(x-1)$ which can also be written as $y=8-3x$.
5. This must be $y=2x+c$ for some constant $c$, and the line goes through $(3,5)$ so $5=6+c$ and so the line is $y=2x-1$.
6. I might try to show that all the sides are the same length, and that all the corners are right angles. First I need to draw a diagram to get the points in the right order.
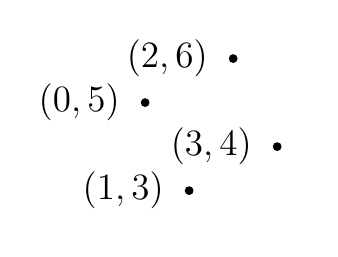
Now I can check that the distances from $(1,3)$ to $(3,4)$, from $(3,4)$ to $(2,6)$, from $(2,6)$ to $(0,5)$, and from $(0,5)$ to $(1,3)$ are all $\sqrt{5}$.
To check the corners are right angles, I could check that the gradients of the lines for each side multiply to $-1$. Those gradients are all either $\frac{1}{2}$ or $-2$, so all the corners are right angles.
7. There are lots of examples that work! I decided to use the $x$-axis as one of my lines (that's $y=0$), and then use something like $y=\sqrt{3}-ax$ and $y=\sqrt{3}+bx$ for some $a$ and $b$; I've chosen those $y$-intercepts so that $(0,\sqrt{3})$ is a corner of the triangle.
I need those two lines to go through $(\pm 1,0)$. I can do that by choosing $a$ and $b$ carefully, and I end up with the three lines $y=0$ and $y=\sqrt{3}(1-x)$ and $y=\sqrt{3}(1+x)$.
8. $(x+1)^2+(y-2)^2=3^2$
The area is $\pi r^2$ and $r=3$ so the area is $9\pi$.
The circle meets the $x$-axis where $(x+1)^2+(0-2)^2=3^2$. That's $x=-1\pm \sqrt{5}$.
The circle meets the $y$-axis where $(0+1)^2+(y-2)^2=3^2$. That's $y=2\pm\sqrt{8}$.
9. $x^2+9x+y^2-3y=\left(x+\frac{9}{2}\right)^2+\left(y-\frac{3}{2}\right)^2-\frac{81}{4}-\frac{9}{4}$. The equation of the circle is $\left(x+\frac{9}{2}\right)^2+\left(y-\frac{3}{2}\right)^2=10+\frac{90}{4}$. So the centre is $\left(-\frac{9}{2},\frac{3}{2}\right)$ and the radius is $\sqrt{\frac{65}{2}}$.
10. Draw a diagram.
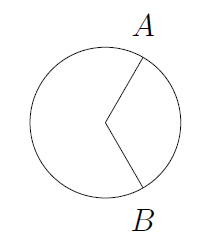
Since $120^\circ$ is one-third of $360^\circ$, the length of the arc is one-third of the length of the circumference $2\pi r$ with $r=2$. So the length of the arc is $\frac{4}{3}\pi$. The area is one-third of $\pi r^2$, which works out to be $\frac{4}{3}\pi$.
11. Draw a diagram.
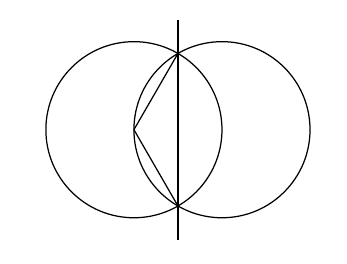
Find the points of intersection. Taking the difference between the two equations gives $x^2=(x-2)^2$, so $x=2-x$ or $x=x-2$, which only has $x=1$ as a solution. The $y$-coordinates are $\pm \sqrt{3}$, and the angle at the centre is $120^\circ$. Let's aim to find the area to the right of $x=1$ that's inside both circles. That's the area of the sector from the previous question, minus the area of a triangle. We can use $\frac{1}{2}ab \sin\theta$ to work out the area of the triangle, $\sqrt{3}$.
Then we'll need to double the area to get our final answer of $\frac{8}{3}\pi -2\sqrt{3}$.
12. Draw a diagram.
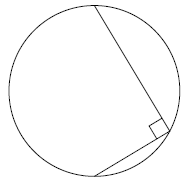
We could write down equations for the distance of a general point $(x,y)$ to each of these points and set them equal to each other, but that's a lot of work.
Instead, note that the gradient of the line from $(0,0)$ to $(1,a)$ is $a$ and the gradient of the line from $(1,a)$ to $(0,a+a^{-1})$ is $-a^{-1}$. These gradients multiply to $-1$, so the lines are at right-angles.
The angle in a semi-circle is a right-angle, so the line from the first point to the third point is the diameter of the circle.
The centre is at the midpoint of the diameter, so it's at $(0,\frac{1}{2}\left(a+a^{-1}\right))$.
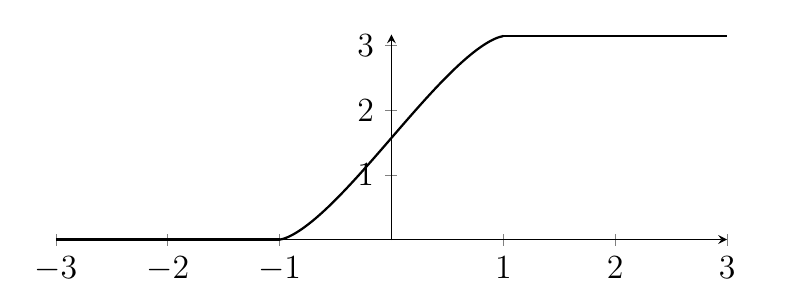
13. The area $A(c)$ is zero if $c<-1$ and it's $\pi$ if $c>1$. In between, the area rises from 0 to $\pi$ in a nice symmetric manner; slow then fast then slow.
MAT 2008 Q4
(i) Let's write down $(x-a)^2+(y-b)^2=r^2$ for the equation of the circle. The three points $(0,0)$ and $(p,0)$ and $(0,q)$ all lie on the circle, which gives three equations;
\begin{equation*}
(0-a)^2+(0-b)^2=r^2, \qquad (p-a)^2+(0-b)^2=r^2, \qquad (0-a)^2+(q-b)^2=r^2.
\end{equation*}
We can simplify these a bit, and multiply out some squares, and take the difference between pairs of equations, to get
\begin{equation*}
p^2-2pa=0,\qquad q^2-2qb=0,\qquad a^2+b^2=r^2
\end{equation*}
Now $p\neq 0$ and $q\neq 0$ so $a=\frac{p}{2}$ and $b=\frac{q}{2}$, and $\displaystyle r=\sqrt{\frac{p^2+q^2}{4}}$.
If we substitute those numbers into the equation $(x-a)^2+(y-b)^2=r^2$ and multiply out the squares, we get the equation in the question.
Along the way, we found the centre $(a,b)=\left(\frac{p}{2},\frac{q}{2}\right)$ and we found the radius. The area of $C$ is $\displaystyle \pi\frac{p^2+q^2}{4}$.
(ii) We just found the area of the circle. The area of the triangle is $\frac{1}{2}pq$. If we write out the inequality in the question, we see that we're being asked to prove that
$$
\pi\frac{p^2+q^2}{2pq}\geq \pi
$$
for all positive real numbers $p$ and $q$. This is true because $(p-q)^2\geq 0$, and that rearranges to the inequality above (we can divide by $pq$ because $p$ and $q$ are not zero). If I'm honest, I rearranged the equation first, factorised it as $(p-q)^2$, realised that was positive or zero, then presented all of that to you in the opposite order. Sometimes it's a good idea to work backwards as well as forwards... provided that your final argument makes sense, of course.
(iii) Now we're asked to solve
$$
\pi\frac{p^2+q^2}{2pq}=2\pi
$$
which rearranges to $p^2+q^2=4pq$. This is one equation for two variables, so we can't really solve it for $p$ and $q$. But we just want expressions for the angles. From trigonometry, we know that $q/p$ is $\tan\angle OPQ$, and something similar is true for $\tan \angle OQP$. That inspires me to divide the equation by $p^2$ and solve
\begin{equation*}
1+\left(\frac{q}{p}\right)^2=4\left(\frac{q}{p}\right)
\end{equation*}
which is just a quadratic equation. The roots are $2\pm\sqrt{3}$ so the angles are $\tan^{-1} \left(2\pm \sqrt{3}\right)$.
Extension
- If $\tan\theta=2-\sqrt{3}$ then $$\tan 2\theta = \frac{4-2\sqrt{3}}{1-\left(4-4\sqrt{3}+3\right)}=\frac{4-2\sqrt{3}}{4\sqrt{3}-6}=\frac{1}{\sqrt{3}}$$
so $2\theta$ is $30^\circ$ (restricting to the range $0\leq \theta\leq 180^\circ$). So $\theta$ must be $15^\circ$.
If $\tan\theta=2+\sqrt{3}$ then $$\tan 2\theta = \frac{4+2\sqrt{3}}{1-\left(4+4\sqrt{3}+3\right)}=\frac{4+2\sqrt{3}}{-4\sqrt{3}-6}=-\frac{1}{\sqrt{3}}$$
so $2\theta$ is $150^\circ$ (restricting to the range $0\leq \theta\leq 180^\circ$). So $\theta$ must be $75^\circ$. - Differentiate to get $1-x^{-2}$ which is zero at $x=\pm 1$. The minimum value of the function occurs when $x=1$, and the value is $2$.
Alternatively, use the fact that $a^2+b^2\geq 2ab$ with $a=x^{1/2}$ and $b=x^{-1/2}$. Then $x+x^{-1}\geq 2x^{1/2}x^{-1/2}=2$.
MAT 2010 Q4
(i) If I drop a perpendicular from $(1,2h)$ to $(1,0)$ then I have a right-angled triangle with angle $\theta$, opposite a side of length $2h$ and adjacent to a side of length $2h$. So $\tan\theta=2h$.
(ii) $(1,2h)$ lies in $x^2+y^2<4$ if and only if $1+4h^2<4$, which rearranges to $h^2<\frac{3}{4}$. Since $h>0$, this condition is equivalent to $h<\sqrt{3}/2$.
(iii) The gradient of the line is $-h$ because the $y$-value changes by $-2h$ between $x=1$ and $x=3$. The line goes through $(3,0)$ and has equation $y=-h(x-3)$.
We could look for repeated roots between $x^2+y^2=4$ and $y=-h(x-3)$. In general if I substitute one into the other I get $x^2+h^2(x-3)^2=4$. If $h=2/\sqrt{5}$ then this is $5x^2+4(x-3)^2=20$. If we multiply this out, rearrange, and factorise, we get $(3x-4)^2=0$ indicating that there is a double root at $x=4/3$, so the line is tangent to the circle.
(iv) In this case, the point $(1,2h)$ is outside the circle, because $\frac{2}{\sqrt{5}}>\frac{\sqrt{3}}{2}$ (I know this because $\frac{4}{5}>\frac{3}{4}$). The diagram is like the first picture in the question. The area inside both is the area of the sector with angle $\theta$. So the area is $\displaystyle 4\pi \frac{\theta}{360^\circ}$ where $\tan\theta=2h$.
(v) In this case, the point $(1,2h)$ is inside the circle, because $\frac{6}{7}<\frac{\sqrt{3}}{2}$ (I know this because $\frac{36}{49}<\frac{3}{4}$ (I know this because $144<147$)). The diagram is like the second picture in the question.
Check that $(8/5,6/5)$ lies on the circle; $(8/5)^2+(6/5)^2=(64/25)+(36/25)=4$. Check that $(8/5,6/5)$ lies on the line; $-\frac{6}{7}\left(\frac{8}{5} - 3\right)=\frac{6}{5}$.
The area is made up of a triangle with corners $(0,0)$ and $(1,12/7)$ and $(8/5,6/5)$, plus a sector of a circle from the $x$-axis up to the line from the origin to $(8/5,6/5)$.
Using the formula in the question, the area of the triangle is $\displaystyle \frac{27}{35}$. The area of the sector is $\displaystyle 4\pi\frac{\alpha}{360^\circ}$ where $\displaystyle \tan\alpha=\frac{6}{8}$. Add these.
Extension
- Let $A$ be $(a,b)$ and let $C$ be $(c,d)$ and let $M$ be $(a,0)$ and let $N$ be $(c,0)$. The area we want is the triangle $OCN$ plus the trapezium $NCAM$ minus the triangle $OAM$. If we find all of these and simplify, we get $\frac{1}{2}\left(ad-bc\right)$. The absolute value signs come in because I haven't been very careful; I've assumed that $(a,b)$ and $(c,d)$ are a particular way around.
- Consider the cross product of the vectors $(a,b,0)\times (c,d,0)=(0,0,ad-bc)$. We also know that the magnitude of $\mathbf{a}\times \mathbf{b}$ is $|\mathbf{a}| |\mathbf{b}| \sin\theta$, which is (almost) exactly the formula for the area of the triangle. So we just need to take the magnitude of $\mathbf{a}\times \mathbf{b}$ and divide by 2 to get the area of the triangle.

