Trigonometry Solutions

Part of the Oxford MAT Livestream.

Revision Questions

1. Split the equilateral triangle into two right-angled triangles.

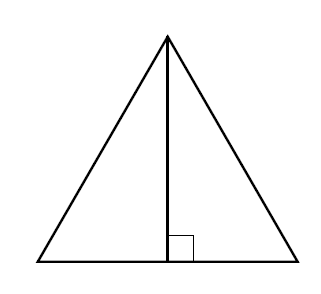
Each has base $\displaystyle\frac{a}{2}$ and height $\displaystyle\frac{\sqrt{3}a}{2}$, so the total area is $\displaystyle \frac{\sqrt{3}a^2}{4}$.

2. From the graph of $\sin x$, we expect two solutions in that range. If I draw a little triangle with opposite side 1 and hypotenuse 2 then I recognise this as half an equilateral triangle (so one solution is $30^\circ$, then using $\sin(180^\circ-x)=\sin x$ another is $150^\circ$).

3. From the graph of $\tan x$, we expect solutions to be $45^\circ+180^\circ n$ for any whole number $n$. In the given range, this is $x=45^\circ$ or $x=225^\circ$.

4. If we write $u=45x$ then we've got $\tan (u)=1$ so $u=45^\circ+180^\circ n$ just like in the previous part. But careful, because if $45x=45^\circ+180^\circ n$ then $x=1^\circ + 4^\circ n$, so the solutions are the angles $1^\circ, 5^\circ, 9^\circ,\dots,357^\circ$, not just $1^\circ$ and $5^\circ$.

5. Let's draw a picture

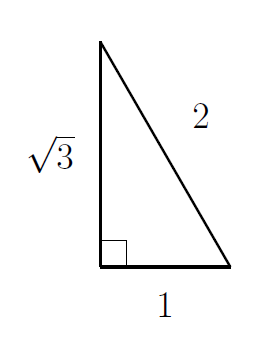
The area formulas give me the area as 
$$
\frac{1}{2}\times 1 \times \sqrt{3} \times \sin 90^\circ \quad \text{or}\quad \frac{1}{2}\times \sqrt{3} \times 2 \times \sin 30^\circ \quad \text{or}\quad\frac{1}{2}\times 1 \times 2 \times \sin 60^\circ
$$
all of which are equal to $\sqrt{3}/2$.

6. First I can expand the square to get $\cos^2 x + 2\cos x \sin x + \sin^2 x$.

Now I can use $\cos^2 x+ \sin^2 x=1$ and I can write $2\cos x \sin x$ as $2u$.

So the expression is $2u+1$.

7. This is a geometric series with first term $a=1$ and common ratio $r=-\sin^2x$, so the sum to infinity is $(1+\sin^2 x)^{-1}$ which is $(2-\cos^2 x)^{-1}$ in terms of $\cos x$.

The sum only converges if the common ratio $r$ satisfies $|r|<1$. This is not the case if $x=90^\circ$.

8. I'll use $\cos^2 x=1-\sin^2 x$ and substitute this into the expression.

$\cos^4x+\cos^2x=(1-\sin^2 x)^2+(1-\sin^2 x)=2-3\sin^2 x+\sin^4 x$.

9. $\cos(450^\circ-x)=\cos(90^\circ-x)$ using the fact that $\cos x$ is periodic with period $360^\circ$.

Then $\cos(90^\circ-x)=\sin x$.

10. We can use $\cos(90^\circ-x)=\sin x$ and $\sin(90^\circ-x)=\cos x$, and also $\sin(180^\circ-x)=\sin x$ and $\cos(180^\circ -x)=-\cos x$.

We have $(\sin x)(\sin x)-(\cos x)(-\cos x)=\sin^2 x+\cos^2 x=1$.

11. Use the cosine rule: $|AC|^2=3^2+2^2-2\times 3 \times 2 \times \cos 120^\circ$, so $|AC|=\sqrt{19}$.

Use the $\frac{1}{2}ab\sin \gamma$ formula for the area: $\frac{1}{2}\times 3 \times 2 \times \sin 120^\circ=\frac{3\sqrt{3}}{2}$.

Use the sine rule: $\displaystyle\frac{\sin 120^\circ}{\sqrt{19}}=\frac{\sin \angle BCA}{3}$ so $\displaystyle\sin\angle BCA=\frac{3\sqrt{3}}{2\sqrt{19}}$

12. The cosine rule is $a^2=b^2+c^2-2bc\cos \alpha$.

Since $-1\leq \cos \alpha\leq 1$, we have $b^2-2bc+c^2\leq b^2+c^2-2bc\cos \alpha\leq b^2+2bc+c^2$.

So $(b-c)^2\leq a^2 \leq (b+c)^2$. Since $a>0$ and $(b+c)>0$, it follows that $a\leq b+c$.

In fact, we can't actually have $a=b+c$ because that would be a triangle with a $180^\circ$ angle. So $a<b+c$.

13. If we write down the cosine rule for each of the angles, we get
\begin{alignat*}{12}
8^2&=&13^2&+&15^2&-&2&\times& 13 &\times& 15 &\times& \cos \alpha\\
13^2&=&15^2&+&8^2&-&2&\times& 15 &\times& 8 &\times& \cos \beta\\
15^2&=&8^2&+&13^2&-&2&\times& 8 &\times& 13 &\times& \cos \gamma
\end{alignat*}
and these rearrange to
\begin{equation*}
\cos \alpha =\frac{11}{13},\quad \cos \beta=\frac{1}{2},\quad \cos \gamma =\frac{1}{26}
\end{equation*}
from which we see that $\beta=60^\circ$.

MAT 2007 Q4

(i) The centre of the circle is at $(1,1)$, because the radius is 1, and that's the distance from the centre to each axis (measuring from the centre to each axis).

I drew a line from $Q$ to the centre of the circle.

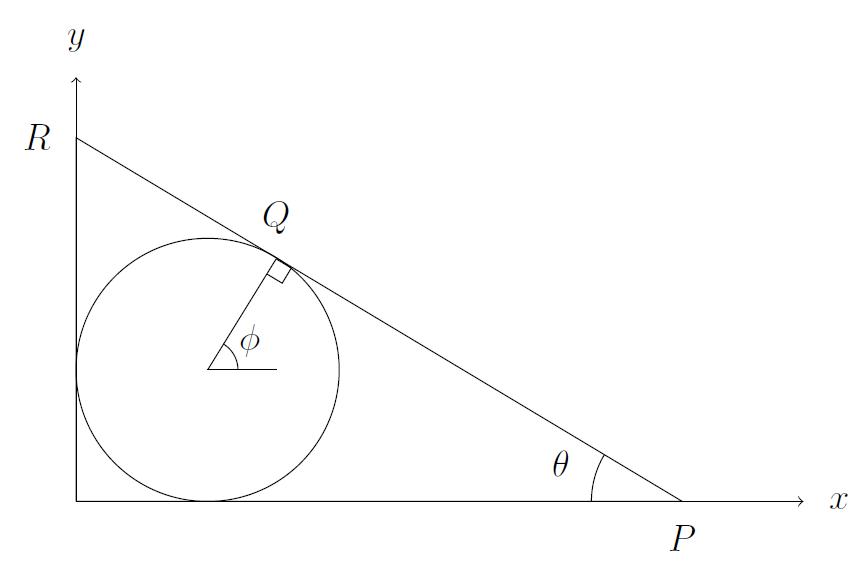
I've called the angle that line makes with the positive-$x$ direction $\phi$. Because the tangent is at right angles to the radius, we have $\phi=90^\circ-\theta$. A little bit of trigonometry, using the fact that the radius of the circle is 1, gives the coordinates of $Q$ as $(1+\cos \phi,1+\sin\phi)$. Then I can convert this to the expression in the question by using $\cos(90^\circ -\theta)=\sin \theta$ and $\sin(90^\circ - \theta)=\cos \theta$.

The gradient of $PQR$ is the change in $y$ divided by the change in $x$. If I write $|PR|$ for the length of the hypotenuse of the right-angled triangle $OPR$, then the gradient is $$ \frac{-|PR| \sin \theta}{|PR| \cos \theta}.$$ This simplifies to $-\tan \theta$.

The line has gradient $-\tan \theta$ and goes through $(1+\sin\theta,1+\cos\theta)$. So the equation of the line is
$$
y=-\tan\theta \left(x-1-\sin\theta\right)+1+\cos\theta
$$
The $x$-intercept of this line is at 
$$
x=1+\sin\theta +\frac{1+\cos\theta}{\tan\theta}
$$
and that's the $x$-coordinate of $P$. The $y$-coordinate of $P$ is just zero.

(ii) Draw two diagrams, one with $\theta$ as in the question, and one with $90^\circ -\theta$ instead.

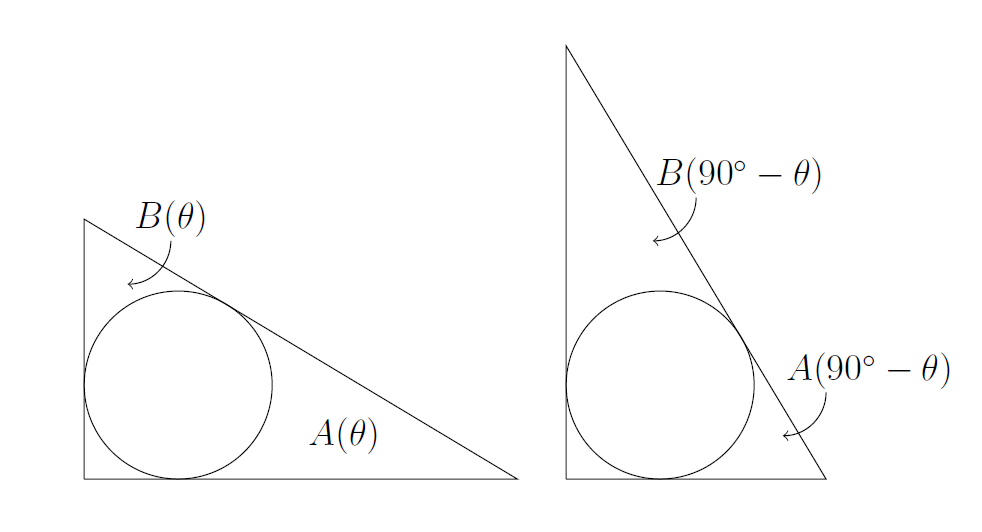
The second diagram is just a reflection of the first diagram. The angles match because the angles in a triangle add up to $180^\circ$. So the region marked $A(\theta)$ in the first diagram has the same area as the region marked $B(90^\circ-\theta)$ in the second diagram.

We can use this to calculate $A(45^\circ)$. In this case $B(45)=A(90^\circ-45^\circ)=A(45^\circ)$ so the $A$ and $B$ regions have the same area. My strategy now is to draw some lines from the centre of the circle to the sides of the axes, and to write the total area of the triangle as a square plus three-quarters of a circle plus $A(45^\circ)$ plus $B(45^\circ)$.

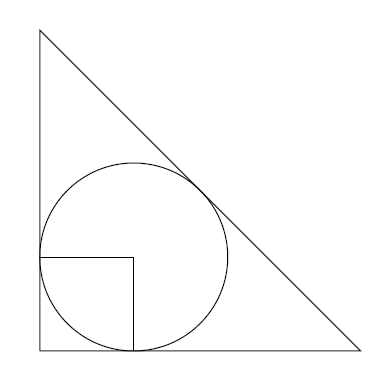
I'll need to know the side length of the triangle. This is just the $x$-coordinate of $P$, which we found above. For $\theta=45^\circ$, this is $2+\sqrt{2}$. So
$$
A(45^\circ)=\frac{1}{2}\left(\frac{(2+\sqrt{2})^2}{2}-1-\frac{3\pi}{4}\right)=1+\sqrt{2}-\frac{3\pi}{8}
$$

(iii) For this part I'll draw a line joining the centre of the circle to $P$.

The area $A(60^\circ)$ is made of two triangles, minus the sector of a circle. Using the fact that the radius is 1 and the $60^\circ$-angle at $P$ is split into equal parts (congruent triangles) by the line to the centre of the circle, we see that the area of each triangle is $\displaystyle \frac{1}{2\tan 30^\circ}$. The angle at the centre of the circle is $120^\circ$, so the area of the sector is $\displaystyle\frac{\pi}{3}$. This gives the final answer in the question.

Extension

• We can adapt the strategy above to find the area as $$A(\theta)=\frac{1}{\tan (\theta/2)}-\pi\frac{\left(180^\circ - \theta\right)}{360^\circ}.$$
  Alternatively, use the $x$-coordinate of $P$ to get the equivalent expression
  $$A(\theta)=\sin \theta +\frac{1+\cos \theta}{\tan \theta}-\pi\frac{\left(180^\circ - \theta\right)}{360^\circ}.$$

MAT 2012 Q4

(i) The gradient is the change in $y$ divided by the change in $x$. Here, we're moving from $(0,2)$ to $(x,x^2)$ so the change in $y$ is $x^2-2$ and the change in $x$ is $x-0$. The gradient is
$$
\frac{x^2-2}{x}.
$$

(ii) The tangent to the parabola at $B$ is the same thing as the tangent to the circle at $B$, because the circle and parabola are tangential to each other. The tangent to the parabola has gradient $2x$. We found the gradient of the radius of the circle at $B$ in the previous part. The tangent is at right angles to the radius for a circle, and if two lines are at right angles then their gradients multiply to give $-1$. So to find the $x$-coordinate of $B$ we need to solve
$$
\left(\frac{x^2-2}{x}\right)\left(2x\right)=-1.
$$
This rearranges to $2x^2=3$ and we want the positive root for $B$ (the negative root gives $A$). Remember that the $y$-coordinate is the square of the $x$-coordinate because $B$ lies on the parabola.

(iii) We could aim to find an angle at the centre of the circle.

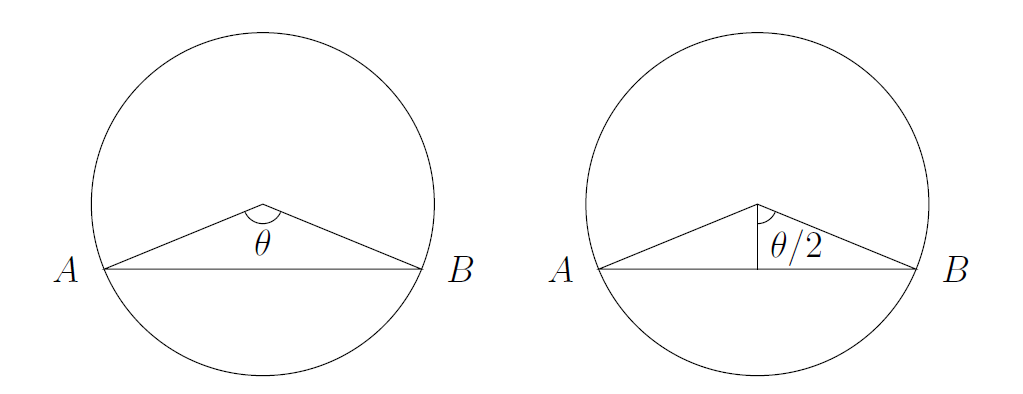
There are two ways we might do this, and both of them involve angles. We might find all the lengths of the sides of the triangle in that diagram, and apply the cosine rule to find $\theta$. Or we might split the triangle in two by dropping a perpendicular from the centre down to the opposite side. If we do that, we can find two side lengths which define $\cos(\theta/2)$. If you used the second method, you probably didn't call the angle $\theta/2$.

Either way, we need the distance from the centre to $B$, the radius of the circle. We know the coordinates of both points, so this is just a matter of applying Pythagoras' theorem to find the radius as
$$
r=\sqrt{\left(\sqrt{\frac{3}{2}}\right)^2+\left(\frac{3}{2}-2\right)^2}=\frac{\sqrt{7}}{2}.
$$

(iv) Returning to the algebra in parts (i) and (ii), we see that we need there to be solutions to
$$
\left(\frac{x^2-a}{x}\right)(2x)=-1
$$
This rearranges to $2x^2=2a-1$, which has two distinct solutions (for $A$ and $B$) if and only if $a>\frac{1}{2}$.

If $a\leq \frac{1}{2}$ then there are no solutions for $A$ and $B$ and the circle must instead be resting on the parabola at the origin (the vertex of the parabola).

(v) In the first case, we can adapt some of the algebra above to find the radius as
$$
r=\sqrt{\left(\sqrt{\frac{2a-1}{2}}\right)^2+\left(\frac{2a-1}{2}-a\right)^2}=\sqrt{a-\frac{1}{4}}.
$$

In instead the circle is resting on the vertex, then the radius is just $r=a$ because the distance between the centre and the origin is just $\sqrt{(0-0)^2+(a-0)^2}$.

Extension

• $\displaystyle \cos2\theta=2\left(\frac{1}{7}\right)-1=-\frac{5}{7}$. The two expressions are equivalent; one of them just involves an angle that is twice as large as the other.
• The result is very similar to the question on the Algebra sheet. A circle is the points that area a particular distance from a point, so the circle that "rests" on the parabola identifies the points that are at the minimum distance from the centre of the circle. With the centre of the circle on the $y$-axis, this is similar to the calculation we did before with points above or below the point $\left(0,\frac{1}{2}\right)$.