Algebra
Part of the Oxford MAT Livestream.
MAT syllabus
Simple simultaneous equations in one or two variables. Solution of simple inequalities. Binomial Theorem with positive whole exponent. Combinations and binomial probabilities.
Revision
- Given two linear equations for $x$ and $y$ like $2x+3y=7$ and $3x+5y=9$, we can solve by rearranging the first for $x$ and substituting that into the second equation, then rearranging the resulting equation for $y$, before back-substituting for $x$.
- We can add and subtract from each side of an inequality. For example, if $x<2$ then $x+3<2+3$, and if $y>-3$ then $y-5>-3-5$.
- We can multiply each side of an inequality by a number, but if we multiply by a negative number then the direction of the inequality changes. For example, $-6<-3$, but when we multiply both sides by $-\frac{1}{3}$ we need to flip the sign to get the true statement $2>1$.
- Squaring each side of an inequality is a bit like multiplying, and we need to be careful. If both sides of an inequality are positive, then squaring each side preserves the inequality, because $x^2$ is an increasing function when $x>0$.
- If we have a quadratic inequality like $(x+3)(x-5)<0$, then we can consider the signs of the terms. In this case the inequality is satisfied for $-3<x<5$.
- (Binomial Theorem) If $n$ is a positive whole number then
$$(x+y)^n=x^n+nx^{n-1}y+\dots+\binom{n}{r} x^r y^{n-r}+\dots+nxy^{n-1}+y^n$$
where $\displaystyle \binom{n}{r} = \frac{n!}{r!(n-r)!}$ and $n!$ means $n\times (n-1)\times (n-2)\times\dots \times 2 \times 1$ for a whole number $n$. - (Combinations) Given a set of $n$ different items, there are $\displaystyle \binom{n}{r}$ subsets of size $r$.
Proof: suppose we list the $n$ items and take the first $r$ items on the list. There are $n!$ ways to list the items, but we've over-counted the subsets of size $r$ because it doesn't matter what order the $r$ items are in, and it doesn't matter what order the other $(n-r)$ items are in. The way to fix this over-counting is to divide. Each subset of size $r$ has been counted $r!(n-r)!$ times; the first factorial allows for all the separate orders of the $r$ items, and the other allows for all the orders of the $(n-r)$ items. So we have $\displaystyle \frac{n!}{r!(n-r)!}$ subsets. - If we're selecting items for an ordered list then we should only allow for the over-counting of the irrelevant orderings of the $(n-r)$ other items, so the number of ordered lists containing $r$ items from a set of $n$ is $\displaystyle\frac{n!}{(n-r)!}$.
- (Binomial probabilities) If $n$ independent events each have probability $p$ of success and probability $q$ of failure, with $p+q=1$, then the probability of exactly $r$ successes is $\displaystyle\binom{n}{r} p^rq^{n-r}$ for $0\leq r \leq n$.
Revision Questions
- Solve the simultaneous equations $x+4y=1$ and $2x-y=3$.
- Solve the simultaneous equations $x^2+2x+xy+y^2=5$ and $x+y=2$.
- Solve the simultaneous equations $x^2+y=2$ and $x+y^2=2$.
- Expand $(2x+3y)^3$
- What is the coefficient of the $x^2$ term in the polynomial $w(x) = (3x - 1)^4$?
- What is the sum of the coefficients of the polynomial $(x + 2)^{3}$? What about $(x+2)^{300}$?
- For which values of $x$ is it true that $x^2+4x+3>0$?
- Given $-2<a<1$, what can you say about $a^2$?
- Given $a<b$ and $c<d$, what (if anything) can you say about the relationship between $ac$ and $bd$? What (if anything) can you say if you're also told that $a>0$ and $c>0$?
- I'm going to flip five fair coins (each is heads or tails with equal probability, and each is independent of the others). What's the probability that I get exactly three heads?
- I've got six cards that have the numbers one to six on them. I'm going to shuffle them and then deal them out from left to right. What's the probability that the cards alternate between odd and even numbers (either starting with an odd number or an even number, then switching between odd and even for each subsequent card)?
- A game show has 10 contestants, and three finalists are chosen at random. What is the probability that contestant 1 is a finalist and contestant 2 is not?
- A class has 20 students, 10 boys and 10 girls. If the teacher randomly selects 4 students to answer a question, what is the probability that exactly three of them are girls?
- A multiple-choice test has 10 questions, each with 5 answer choices. If you guess on every question, what is the probability of getting at least 8 questions correct?
MAT Questions
MAT 2014 Q1A
The inequality $$ x^4<8x^2+9 $$ is satisfied precisely when
(a) $-3<x<3$,
(b) $0<x<4$,
(c) $1<x<3$,
(d) $-1<x<9$,
(e) $-3<x<-1$.
Hints
- Start by thinking about values of $u$ for which $u^2<8u+9$.
- Next, think about the values that $u=x^2$ takes as $x$ varies.
- Sketch graphs of the functions on each side of the inequality to check your answer.
MAT 2014 Q1G
Let $n$ be a positive integer. The coefficient of $x^{3}y^{5}$ in the expansion of $$(1+xy+y^{2})^{n}$$ equals
(a) $n$,
(b) $2^n$,
(c) $\displaystyle \binom{n}{3} \binom{n}{5}$,
(d) $\displaystyle 4\binom{n}{4}$,
(e) $\displaystyle \binom{n}{8}$.
Hints
- The Binomial Theorem lets us expand $(A+B)^n$ where $A$ is anything and $B$ is anything. This question tests that by putting $x$ and $y$ in unusual places.
- $1+xy+y^2=1+(xy+y^2)$
- There's only one value of $k$ such that $x^3y^5$ appears in the expansion of $(xy+y^2)^k$.
MAT 2015 Q2
(i) Expand and simplify $$(a-b)(a^n+a^{n-1}b + a^{n-2}b^{2} + \dots + ab^{n-1} + b^n).$$
(ii) The prime number $3$ has the property that it is one less than a square number. Are there any other prime numbers with this property? Justify your answer.
(iii) Find all the prime numbers that are one more than a cube number. Justify your answer.
(iv) Is $3^{2015} - 2^{2015}$ a prime number? Explain your reasoning carefully.
(v) Is there a positive integer $k$ for which $k^3 + 2k^2 + 2k + 1$ is a cube number? Explain your reasoning carefully.
Hints
(i) We have a choice: expand $a$ times the second bracket and then $(-b)$ times the second bracket, or multiply $(a-b)$ by each term in the second bracket. Either way, we will probably need to simplify our answer. If you do that correctly, it should simplify down significantly!
(ii) Write out an algebraic expression that captures what it means for a number to be "one less than a square number". A prime number is an integer larger than 1 with no factors other than 1 and itself.
(iii) Adapt what you did in the previous part. We'll need to find a factor of $x^3+1$. You can use the first part of the question to write down a factorisation of this expression, if you choose $a$ and $b$ carefully.
(iv) It's tempting to set $a=3$ and $b=2$ and $n=2014$ in the expression we had for the first part of the question. But careful; $(3-2)=1$, and that's a trivial factor. Prime numbers are allowed to have 1 as a factor!
When you're faced with set-back like this, it's tempting to go far from the beaten track and try something totally different. But before you give up on the expression in the first part, consider if there are other values you could set for $a$ and $b$ and $n$ which also satisfy $3^{2015}=a^n$ and $2^{2015}=b^n$.
(v) It's hard to solve equations like $k^3+2k^2+2k+1=m^3$. Instead, we could think about how large $m$ is compared to $k$. Is $m$ larger than $k$ or smaller than $k$? Lots larger? Lots smaller? About the same? Remember that these are both whole numbers, so if they're not equal then they differ by at least 1.
Extension
[Just for fun, not part of the MAT question]
- If $p$ and $q$ are primes, is $3^{pq}-2^{pq}$ also prime?
- Is there a positive integer $k$ for which $k^3+2k^2+2k+7$ is a cube number? Explain your reasoning carefully.
MAT 2011 Q3 (modified)
The graphs of $y=x^{3}-x$ and $y=m\left( x-a\right) $ are drawn on the axes below. Here $m>0$ and $a\leqslant -1.$
The line $y=m\left( x-a\right) $ meets the $x$-axis at $A=\left(a,0\right) $, touches the cubic $y=x^{3}-x$ at $B$ and intersects again with the cubic at $C$. The $x$-coordinates of $B$ and $C$ are respectively $b$ and $c$, with $a\leqslant b\leqslant c$.
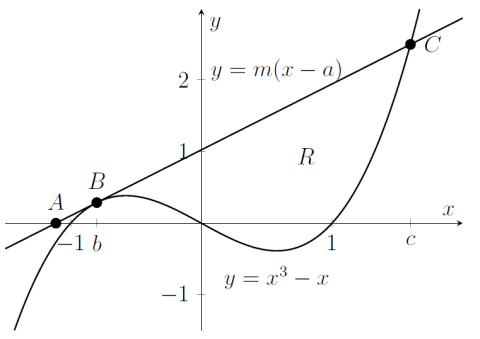
(i) Use the fact that the line and cubic touch when $x=b,$ to show that $m=3b^{2}-1.$
(ii) Show further that
\begin{equation*}
a=\frac{2b^{3}}{3b^{2}-1}.
\end{equation*}
(iii) If $a=-10^{6}$, what is the approximate value of $b$?
(iv) Using the fact that
\begin{equation*}
x^{3}-x-m\left( x-a\right) =\left( x-b\right) ^{2}\left( x-c\right)
\end{equation*}
(which you need not prove), show that $c=-2b.$
(iv) $R$ is the finite region bounded above by the line $y=m\left(
x-a\right) $ and bounded below by the cubic $y=x^{3}-x$. For what value of $a$ is the area of $R$ largest?
Show that the largest possible area of $R$ is $\frac{27}{4}.$
Hints
(i) When a line touches a curve, it's got the same value and the same gradient. We know everything about the cubic, and we'd like to find the gradient and $y$-intercept of the line.
(ii) This part continues the idea that we're deducing facts about the line from the behaviour at $x=b$.
(iii) Let's use the previous part. It might be a good idea to investigate what the graph of $\displaystyle y=\frac{2x^3}{3x^2-1}$ looks like, roughly. Are there any points where the magnitude of $y$ gets really large?
(iv) We've got polynomials on both sides; let's multiply out and compare coefficients, and see what happens.
(v) We should probably do some integration to find that area. You may use the fact that if $f(x)>g(x)$ for $A<x<B$ and $f(A)=g(A)$ and $f(B)=g(B)$ then the area between the curves is $\int_A^B (f(x)-g(x))\,\mathrm{d}x$. We're given an expression for $f-g$ in the previous part of the question.
There's a choice to make here; do we substitute for values of $m$ and $a$, $b$, $c$ in terms of each other first, or do we integrate first and then substitute? My choice would be to replace $c$ with $-2b$ because that's nice and simple, and I would try to get everything in terms of $b$ before integrating.
Extension
[Just for fun, not part of the MAT question]
- Using what you know at the start of part (iv), prove that $$x^3-x-m(x-a)=(x-b)^2(x-c).$$
- Suppose instead that the cubic is $y=x^3-kx$, with $a<\sqrt{k}$ and $a<b<0$. Find the largest possible area of $R$ in terms of $k$.

