Geometry
Part of the Oxford MAT Livestream.
MAT syllabus
Co-ordinate geometry and vectors in the plane. The equations of straight lines and circles. Basic properties of circles. Lengths of arcs of circles.
Revision
- Points in the plane can be described with two coordinates $(x,y)$. The $x$-axis is the line $y=0$, and the $y$-axis is the line $x=0$.
- A vector $\displaystyle \binom{x}{y}$ can store the same information as a pair of coordinates. Used in that sense, the vector is called a position vector.
- A vector can also describe the displacement from one point to another, so that $\displaystyle\binom{2}{1}$ could represent the displacement from $(1,1)$ to $(3,2)$ for example.
- Vectors can be added by adding the components separately. To show that in a diagram, we might interpret the first vector as a position vector (drawing an arrow starting from the origin) and then interpret the second as a displacement (drawing an arrow starting from the end of the first vector).
- The magnitude of the vector $\displaystyle\binom{x}{y}$ is $\sqrt{x^2+y^2}$.
- The distance from $A$ to $B$ is the magnitude of the vector displacement from $A$ to $B$. The distance from \((x_1,y_1)\) to \((x_2,y_2)\) is \(\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\).
- A vector can be multiplied by a number by multiplying each component by that number. The result is a vector in the same direction but with scaled magnitude.
- A straight line has equation $y=mx+c$, where $m$ is the gradient and $c$ is the $y$-intercept. Other ways to write the equation of a line are $ax+by+c=0$ (where that's a different $c$ to the one in the previous expression) or $y-y_1=m(x-x_1)$. The last expression is useful because that line goes through the point $(x_1,y_1)$ and has gradient $m$, which might be information that we've been given.
- Two lines are parallel if and only if they have the same gradient. Two lines are perpendicular if and only if their gradients multiply to give $-1$.
- The equation of the circle with centre $(a,b)$ and radius $r$ is $(x-a)^2+(y-b)^2=r^2$.
- The angle in a semicircle is a right angle; if $AB$ is the diameter of a circle, and $C$ is on the circle, then $\angle ACB=90^\circ$.
- The tangent is at right angles to the radius at any point on a circle's circumference.
- A circle with radius $r$ has area $\pi r^2$ and circumference $2\pi r$.
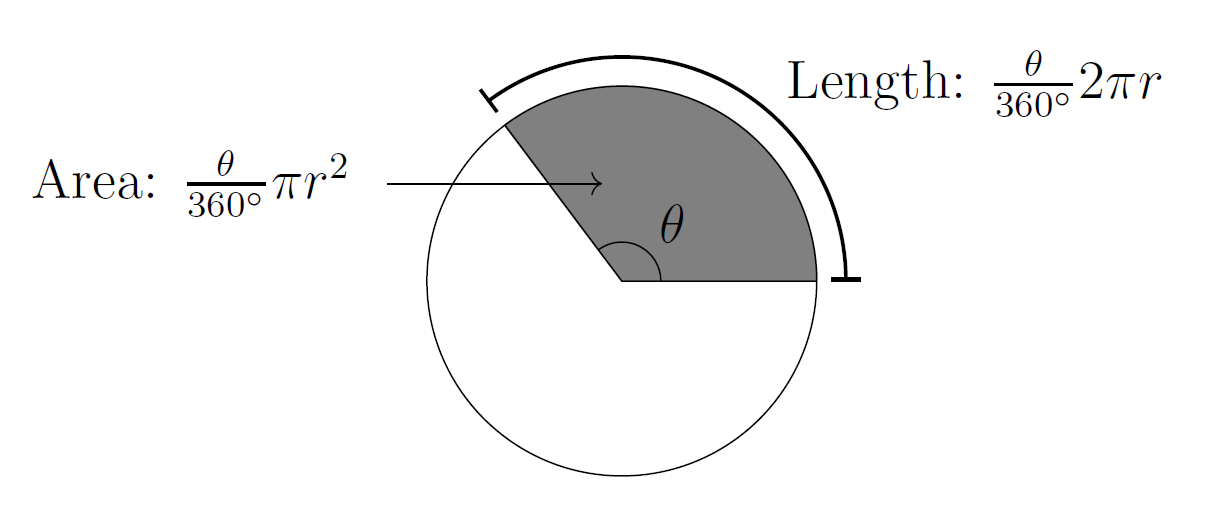
For a circle with radius $r$, suppose that two radii make an angle $\theta$. The arc subtended by $\theta$ has length $\displaystyle\frac{\theta}{360^\circ}2\pi r$.
The area of the sector enclosed by that arc and the radii is $\displaystyle\frac{\theta}{360^\circ}\pi r^2$.
Revision Questions
- Draw a diagram to show the three separate position vectors $\displaystyle \binom{3}{2}$ and $\displaystyle\binom{-4}{1}$ and $\displaystyle\binom{1}{-2}$.
- Add the vectors $\displaystyle \binom{3}{2}$ and $\displaystyle \binom{-4}{1}$. Show this on your diagram.
- Find $\displaystyle 3 \binom{-4}{1}+2\binom{1}{-2}$. Show this on your diagram.
- Find the equation of the line through the points $(1,5)$ and $(3,-1)$.
- Find the equation of the line through the point $(3,5)$ with gradient 2.
- Show that the points $(0,5)$, $(1,3)$, $(2,6)$, and $(3,4)$ lie on the corners of a square.
- Find equations of three lines such that the finite region bounded by the three lines is an equilateral triangle.
- A circle has centre $(-1,2)$ and radius 3. Write down an equation for the circle. What's the area of this circle? Where does this circle cross the axes?
- A circle is given by $x^2+9x+y^2-3y=10$. Find the centre and radius of the circle.
- Points $A$ and $B$ lie on a circle with centre $O$ and radius 2. The angle $\angle AOB$ is 120$^\circ$. Find the length of the arc between $A$ and $B$. Find the area enclosed by that arc and the radii $OA$ and $OB$.
- Two circles are given by $x^2+y^2=4$ and $(x-2)^2+y^2=4$. Find the area of the region that's inside both circles.
- The points $(0,0)$ and $(1,a)$ and $(0,a+a^{-1})$ all lie on the same circle. Find the centre of the circle in terms of $a$.
- A circle has centre $(c,0)$ and radius $1$. The area in the region $x>0$ which is inside the circle depends on $c$, and we'll call it $A(c)$. Sketch a graph of $A(c)$ against $c$.
MAT questions
MAT 2016 Q1C
The origin lies inside the circle with equation $$x^{2}+ax+y^{2}+by=c$$ precisely when
(a) $c>0$,
(b) $a^2+b^2>c$,
(c) $a^2+b^2<c$,
(d) $a^2+b^2>4c$,
(e) $a^2+b^2<4c$.
Hints
- The circle $x^2+ax+y^2+by=c$ is written in quite an unusual way. Where is the centre of this circle? What's the radius?
- Given the location of the centre and the radius, how can you check whether another point is inside the circle?
- If you use the Pythagorean theorem for a distance, be careful with inequalities.
MAT 2017 Q1G
For all $\theta $ in the range $0\leqslant \theta<360^\circ $ the line $$(y-1)\cos\theta = (x+1)\sin\theta$$ divides the disc $x^{2}+y^{2}\leqslant 4$ into two regions. Let $A(\theta )$ denote the area of the larger region.
Then $A(\theta )$ achieves its maximum value at
(a) one value of $\theta$ ,
(b) two values of $\theta$,
(c) three values of $\theta$,
(d) four values of $\theta$,
(e) all values of $\theta$ .
Hints
- The line $(y-1)\cos \theta = (x+1)\sin \theta$ is written in quite an unusual way. Can you find any points that lie on the line?
- Are there any points $(x,y)$ that lie on the line for all values of $\theta$?
- What happens as $\theta$ changes? Sketch some special cases as $\theta$ changes from 0 to $360^\circ$.
- $A(\theta)$ is the area of the "larger" region. Is this region always on the same side of the line?
MAT 2014 Q1D
The reflection of the point $\left( 1,0\right)$ in the line $\ y=mx$ has coordinates
(a) $\displaystyle \left( \frac{m^{2}+1}{m^{2}-1},\frac{m}{m^{2}-1}\right)$ ,
(b) $\displaystyle \left( 1,m\right)$,
(c) $\displaystyle \left( 1-m,m\right)$,
(d) $\displaystyle \left( \frac{1-m^{2}}{1+m^{2}},\frac{2m}{1+m^{2}}\right)$,
(e) $\displaystyle \left( 1-m^{2},m\right)$.
Hints
- The line segment between $(1,0)$ and the reflection of that point should meet the line $y=mx$ at right angles, and the midpoint of the line segment should lie on $y=mx$.
- Two lines are at right angles if their gradients multiply to $-1$.
- If you draw a diagram, you might spot a pair of congruent triangles. Or you could set up some algebra to express the idea that the midpoint lies on the line $y=mx$.
MAT 2008 Q4
Let $p$ and $q$ be positive real numbers. Let $P$ denote the point $(p,0)$ and let $Q$ denote the point $(0,q)$.
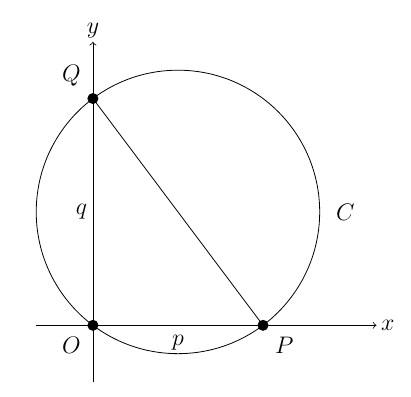
(i) Show that the equation of the circle $C$ which passes through $P$, $Q$, and the origin $O$ is \[ x^2-px+y^2-qy=0.\]
Find the centre and area of $C$.
(ii) Show that \[ \frac{\text{area of circle $C$}}{\text{area of triangle $OPQ$}}\geq \pi\]
(iii) Find expressions for the angles $OPQ$ and $OQP$ if \[ \frac{\text{area of circle $C$}}{\text{area of triangle $OPQ$}}=2\pi\]
Hints
(i) My strategy for this part is to solve in the opposite order; I'll write down an equation for the circle which I'm happy with, and then I'll make it look like the one in the question.
In general the equation for a circle is $(x-a)^2+(y-b)^2=r^2$. We can plug in the points that we know lie on the circle and we'll get equations for $a$ and $b$ and $r$.
To find the centre and radius, I can either rearrange the expression in the question to make it look more like a familiar equation for a circle. Or I could use some of my working above.
Alternatively, draw a right-angle on your copy of the diagram and recall a geometric fact about circles.
(ii) We know expressions for both of these areas in terms of $p$ and $q$. Then we've got an inequality to prove.
To prove an inequality like $a^2+b^2\geq 2ab$, we might move all the terms to one side and try to spot a square (because squares are positive or zero).
(iii) The inequality is now an equality! Time to solve for $p$ and $q$... except we can't. Not entirely, that is. There's a bit of ambiguity because if we double $p$ and also double $q$ then both areas will go up by a factor of 4, so the equality will still hold. At best, we can work out the ratio between $p$ and $q$. This is enough to find the angles in terms of inverse trigonometric functions (can you see why?)
There's another ambiguity; we don't know which way round $P$ and $Q$ are (which one is larger? We don't know). Hopefully, we'll get an equation with at least two solutions.
Extension
[Just for fun, not part of the MAT question]
- Here's an equation for $\tan 2\theta$ (not on the MAT syllabus).
$$\tan 2 \theta=\frac{2\tan \theta}{1-\tan^2\theta}$$
Set $\theta$ to be the value of angle $OPQ$ you found in this question, for which you know the value(s) of $\tan \theta$. Calculate $\tan2\theta$. Deduce the exact value(s) of $\theta$ in degrees. - Find the minimum value of $x+x^{-1}$ for $x>0$.
MAT 2010 Q4 (modified)
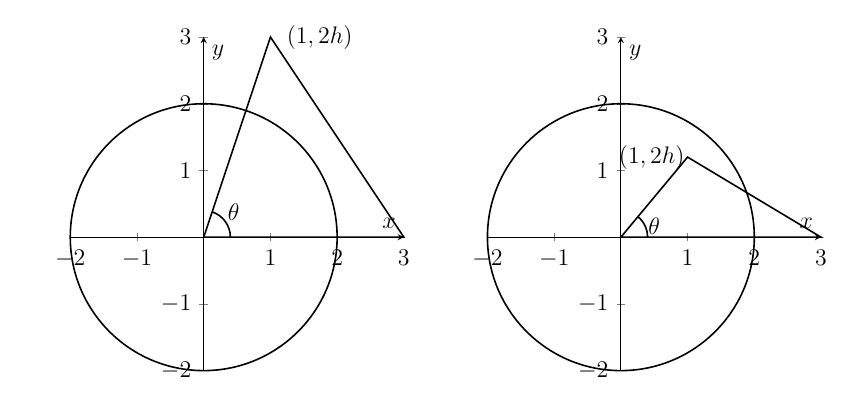
The three corners of a triangle $T$ are $\left( 0,0\right) $, $ \left( 3,0\right) $, $\left( 1,2h\right) $ where $h>0$. The circle $C$ has equation $x^{2}+y^{2}=4$. The angle of the triangle at the origin is denoted as $\theta $. The circle and triangle are drawn in the diagrams above for different values of $h$.
(i) Express $\tan \theta $ in terms of $h$.
(ii) Show that the point $\left( 1,2h\right) $ lies inside $C$ when $h<\sqrt{3}/2.$
(iii) Find the equation of the line connecting $\left( 3,0\right) $ and $\left( 1,2h\right) .$
Show that this line is tangential to the circle $C$ when $h=2/\sqrt{5}.$
(iv) Suppose now that $h>2/\sqrt{5}$. Find the area of the region inside both $C$ and $T$ in terms of $\theta $.
(v) Now let $h=6/7$. Show that the point $\left( 8/5,6/5\right)$ lies on both the line (from part (iii)) and the circle $C.$
Hence show that the area of the region inside both $C$ and $T$ equals
\begin{equation*}
\frac{27}{35}+\frac{\alpha\pi}{90^\circ}
\end{equation*}
where $\alpha $ is an angle in degrees whose tangent, $\tan \alpha $, you should determine.
[You may use the fact that the area of a triangle with corners at $(0,0)$, $(a,b)$, $(c,d)$ equals $\frac{1}{2}|ad-bc|$.]
Hints
(i) Drop a perpendicular line from $(1,2h)$ to the $x$-axis. Your equation for $\tan\theta$ should be nice and simple.
(ii) Points inside the circle have $x^2+y^2<4$, because the distance from such a point to the origin is less than 2. For this question, this is an inequality involving $h$. Try to rearrange it for $h$.
(iii) Careful; the point of tangency is not $(1,2h)$. To be tangential, we would need a single point which is on the line and also on the circle $x^2+y^2=4$.
(iv) In order to get our picture right, we'll need to know whether that point is inside or outside the circle. A good way to compare numbers like $\sqrt{a}/b$ and $c/\sqrt{d}$ is to compare their squares.
Remember that we know the area of a sector of a circle.
(v) This case is different from the previous part. Again, check whether the point $(1,2h)$ lies inside the circle using part (ii). We'll need to compare some square roots again.
The question gives us the coordinates of a point where the line crosses the circle. Mark this on your diagram.
The part of the answer that's a rational number could come from the area of a triangle using the hint at the end of the question. The part of the answer that involves angles and $\pi$ is related to the area of a circle. We might guess that an expression like this comes from the area of a triangle plus the area of a sector.
Extension
[Just for fun, not part of the MAT question]
- If you've learned about the area of a trapezium, drop perpendiculars from $(a,b)$ and $(c,d)$ to the $x$-axis, identify the areas of two right-angled triangles and one trapezium, and deduce the fact about triangle area given in this question.
- If you've learned about the vector product (also known as the cross product), explain the fact about triangle area given in this question.

