Integration Solutions

This resource is part of the 2025 archive of the Oxford MAT Livestream. Click or tap here or on the image below for the new and updated livestream admissions support programme from Oxford Mathematics.

Revision Questions

1. The derivative of $x^a$ is $ax^{a-1}$ so the derivative of this expression is $17x^{16}+17x^{-18}$.
2. Remember that $\sqrt{x}=x^{1/2}$ and $\sqrt[3]{x}=x^{1/3}$, so the derivative of this expression is $x^{-1/2}+x^{-2/3}$, which we could write as \(\displaystyle\frac{1}{\sqrt{x}}+\frac{1}{x^{2/3}}\) if we wanted to.
3. Remember that the derivative of a constant is $0$, so the derivative of this expression is just $-3e^{3x}$.
4. We need to find the value of the derivative $\displaystyle\frac{\mathrm{d}y}{\mathrm{d}x}$ at $x=2$ because that's equal to the gradient of the tangent. We can differentiate to find $\displaystyle\frac{\mathrm{d}y}{\mathrm{d}x}=e^x+2x$ so that gradient we wanted is $e^2+4$. We also want the tangent to have the same value at $x=2$ as the curve; that's $e^x+x^2$ at $x=2$, which is also $e^2+4$. So our tangent is $y=(e^2+4)(x-1)$.
5. First find the derivative at $x=3$, which is $6$ for this parabola. That's the gradient of the tangent, and the normal is at right-angles to the tangent, so it has gradient $\displaystyle -\frac{1}{6}$. We have $\displaystyle y=-\frac{x}{6}+c$ and we want the normal to go through the point $(3,9)$. So we want $\displaystyle c=\frac{19}{2}$.
6. The turning points must have $\displaystyle\frac{\mathrm{d}y}{\mathrm{d}x}=0$ so we must have $4x^3-6x^2+2x=0$. That happens when $x=0$ or when $2x^2-3x+1=0$ which happens when $(2x-1)(x-1)=0$, which is either $x=1$ or $x=\frac{1}{2}$.
   Now find the second derivative to check whether these are minima or maxima. We have $\displaystyle \frac{\mathrm{d}^2y}{\mathrm{d}x^2}=12x^2-12x+2$, which is positive for $x=0$, negative for $x=\frac{1}{2}$, and positive for $x=1$. So we have a (local) minimum, then a (local) maximum, then a (local) minimum.
   The function is decreasing for $x<0$, then increasing for $0<x<\frac{1}{2}$, then decreasing for $\frac{1}{2}<x<1$ then increasing for $x>1$.
7. The line definitely goes through $A$, which doesn't move. The thing we learn from "differentiation from first principles" is that the gradient of the line gets closer and closer to the derivative of the function at $A$.
   The derivative is $3x^2+2x+1$ which is 6 at $x=1$. The value is $4$, so the tangent is $y=6x-2$. So if the line through $A$ and $B$ is $y=mx+c$ then $m$ gets closer and closer to 6 and $c$ gets closer and closer to $-2$.
8. First find the points where $y=0$. We have $(x+3)(x+1)=0$ so these points are at $x=-1$ or $x=-3$. In between, we have $y<0$ (by considering the graph).
   So we want $-\displaystyle \int_{-3}^{-1} x^2+4x+3\,\mathrm{d}x$. That minus sign out the front is because the function is negative in this region. This works out to be $\displaystyle \frac{4}{3}$.
9.  
   • $\displaystyle \int \frac{x+3}{x^3}\,\mathrm{d}x=\int \frac{1}{x^2}+\frac{3}{x^3},\mathrm{d}x=-\frac{1}{x}-\frac{3}{2x^2}+c$ where $c$ is a constant.
   • $\displaystyle \int \sqrt[3]{x}\,\mathrm{d}x=\int x^{1/3}\,\mathrm{d}x=\frac{3}{4}x^{4/3}+c$ where $c$ is a constant.
   • $\displaystyle \int \left(\left(x^2\right)^3\right)^5\,\mathrm{d}x=\int x^{30}\,\mathrm{d}x=\frac{x^{31}}{31}+c$ where $c$ is a constant.
   • $\displaystyle \int \left(x^2+1\right)^3\,\mathrm{d}x=\int x^6+3x^4+3x^2+1\,\mathrm{d}x=\frac{x^7}{7}+\frac{3x^5}{5}+x^3+x+c$ where $c$ is a constant.
10. The graph of $f(-x)$ is the graph of $f(x)$ reflected in $y$-axis. Also, note that if we reflect the interval $-1\leq x \leq 1$ in the $y$-axis then we get the same interval back. On the left-hand side, we're finding the area under $f(x)$ (or maybe negative the area in any regions where $f$ is negative). On the right-hand side, we're calculating exactly the same area, but with the shape of the graph reflected.
11. First consider the graph $\displaystyle y=\frac{1}{x}$. The area under the graph between $x=1$ and $x=10$ is $I_1$. Now consider stretching that region by a factor of 10 parallel to the $x$-axis, and squashing it by a factor of 10 parallel to the $y$-axis. The area will be the same, and (amazingly!) any point that was on the curve $\displaystyle y=\frac{1}{x}$ is still on the graph after these transformations. So $I_2$, the area under the graph between $10$ and $100$ is equal to $I_1$.
    This means that $$\int_1^{100}\frac{1}{x}\,\mathrm{d}x=\int_1^{10}\frac{1}{x}\,\mathrm{d}x+\int_{10}^{100}\frac{1}{x}\,\mathrm{d}x=I_1+I_2=2I_1.$$
    But similarly, if we think about stretching the graph again in the same way, we find that $\displaystyle \int_{100}^{1000}\frac{1}{x}\,\mathrm{d}x$ is also equal to $I_1$. By setting $N$ to be a large power of ten, we can make $\displaystyle \int_1^{N}\frac{1}{x}\,\mathrm{d}x$ arbitrarily large.
12. Note that $\displaystyle \frac{x^2}{1+x^2}+\frac{1}{1+x^2}=1$ so $I_3+I_4=\int_1^3 1 \,\mathrm{d}x=2$. So $I_3+I_4=2$.
13. Note that $\displaystyle \frac{x^4}{1+x^2}=x^2-\frac{x^2}{1+x^2}$ so this new integral is $\displaystyle \int_1^3 x^2\,\mathrm{d}x-I_4=8\frac{2}{3}-I_4$.

MAT Questions

MAT 2017 Q1A

• Stationary points at those values of $x$ for which the derivative of $f(x)$ is zero. So we're looking for points where $6x^2-2kx+2=0$
• We would like to know whether or not there are two distinct values of $x$ that satisfy that equation. It's a quadratic equation.
• We should check the discriminant. If $(2k)^2-4\times 6\times 2>0$ then there are two distinct real solutions.
• That inequality simplifies to $k^2>12$. This is true when either $k>\sqrt{12}$ or when $k<-\sqrt{12}$.
• The answer is (b).

MAT 2018 Q1A

• The curve and the line have the same value where $\sqrt{x}=x-2$. We could square both sides to find that $x=(x-2)^2$, so $x^2-3x+4=0$. The solutions to that equation $x=4$ and $x=1$. But we should check our answers; $\sqrt{1}=1$ and $1-2=-1$, so $x=1$ is not a solution. The point with $x=4$ is a genuine solution, because $\sqrt{4}$ really is equal to $4-2$.
• If we integrate $\sqrt{x}$ from 0 to 4, we would get the area between the curve $\sqrt{x}$ and the $x$-axis, in the region $0<x<4$. We want something slightly different, because we don't want the bit of that area which is under the line $y=x-2$.
• That area under the line $y=x-2$ is a right-angled triangle with base 2 and height 2, so it has area 2. (We could integrate from 2 to 4 to get that area, but I know a formula for the area of a triangle).
• So we just need $\int_0^4 \sqrt{x}\,\mathrm{d}x-2$.
• Time for some integration; $$\int_0^4 \sqrt{x}\,\mathrm{d}x-2=\left[\frac{2}{3}x^{3/2}\right]_0^4-2=\frac{16}{3}-2=\frac{10}{3}.$$
• The answer is (d).

MAT 2018 Q1G

• We can write the second curve as $y=\pm\sqrt{x}$. The curve only exists where $x>0$, and in that region the first curve $y=x^2+c$ has positive gradient. So the gradient will only match if we consider the part of the second curve where $y=+\sqrt{x}$ with a $+$ sign.
• Now we can match up the values of the curves, and separately match up the gradients of the curves, for the system of equations; $$ x^2+c=\sqrt{x},\qquad 2x=\frac{1}{2}\frac{1}{\sqrt{x}}, $$ where by $x$, I mean the particular value of $x$ at the point where the curves meet. (Really I should give that value of $x$ a name, I'm being lazy with my notation here)
• I can solve the second equation for $x=4^{-2/3}$. Then substituting that value into the first equation gives me $c=\sqrt{4^{-2/3}}-\left(4^{-2/3}\right)^2$.
• This simplifies to $c=4^{-1/3}-4^{-4/3}$.
• Most of the options are a single expression, so I'm looking for a way to simplify further. Eventually I spot that $\frac{4}{3}=1+\frac{1}{3}$, so the second term in my expression is $4^{-1}4^{-1/3}$
• So $c=\frac{3}{4}\times4^{-1/3}$
• The answer is (b).

MAT 2009 Q3

(i) The function inside the brackets is $x^3-1$. That's $0$ at $x=1$ and it's $-1$ at $x=0$. It's negative for $x<1$. Here's my sketch of the square of that function, on the left below.

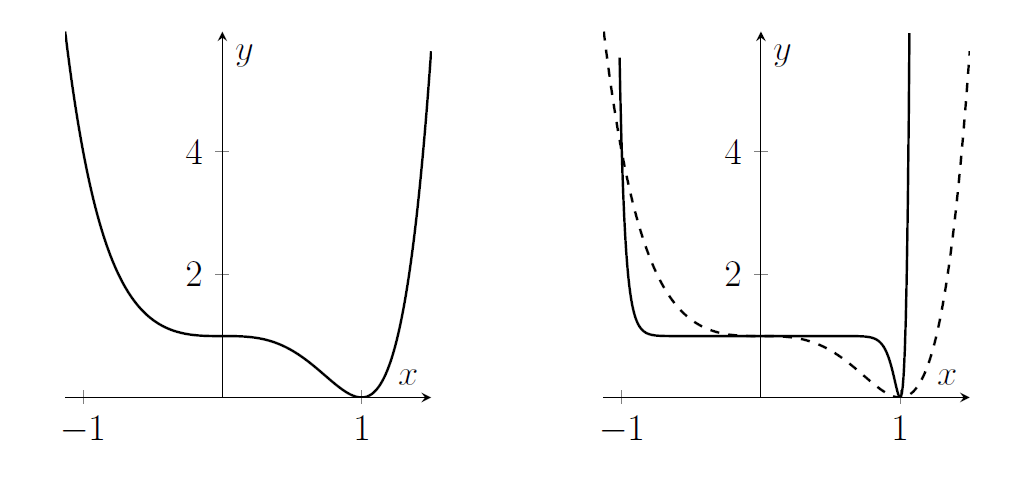
(ii) For higher powers of $n$, the function $x^{2n-1}$ is approximately zero for $|x|<1$, and it grows rapidly outside that range. So $x^{2n-1}-1$ is about $-1$ for the range $|x|<1$, but it shoots up to high positive values soon after $x=1$ and it shoots down to very negative values just before $x=-1$. If we square that function, we'll get something that's about $1$ for most of the range $|x|<1$, but near the edges of that region two strange things will happen. Near $x=-1$, the function inside the brackets just gets really negative. For $x$ near $1$, the function inside the brackets increases to zero then increases to high positive values. For the square of the function, this is a decrease to zero first, then an increase to high positive values. See my sketch above, on the right, with the dashed line indicating my previous sketch.

(iii) We have $$ \int_0^1 f_n(x)\,\mathrm{d}x=\int_0^1 x^{4n-2}-2x^{2n-1}+1\,\mathrm{d}x=\left[\frac{x^{4n-1}}{4n-1}-\frac{x^{2n}}{n}+x\right]_0^1=\frac{1}{4n-1}-\frac{1}{n}+1$$
where the contributions from the lower limit $x=0$ are all zero because those powers of $x$ give zero for $n\geq 1$ a whole number.

(iv) We would like $$ 1+\frac{1}{4n-1}-\frac{1}{n}\leq 1-\frac{A}{n+B}$$ for all $n\geq 1$. This rearranges (being careful not to multiply by negative numbers) to the inequality $$ 0\geq (4A-3)n^2+(1-A-3B)n+B $$
If the coefficient of $n^2$ is positive, this clearly doesn't work (because the right-hand side will get really large and positive for large enough $n$), so we must have $A\leq 3/4$.

(v) If the coefficient of $n^2$ is zero, then $A=3/4$. We still need $$ 0\geq \left(\frac{1}{4}-3B\right)n+B$$ for all $n\geq 1$. For this to work, the linear function on the right-hand side must have negative or zero gradient, and the value at $n=1$ must be negative or zero. We therefore require both $B\geq 1/12$ and also $B \geq 1/8$. Since we need both of these to hold, we must have $B\geq 1/8$.

Quick check that if $A=3/4$ and $B=1/8$ then the inequality is in fact true.

Extension

• If $n=1/2$ then the function is constant and zero. The integral is zero.
• We need $n> 1/4$. If $n\leq 1/4$ then the integral doesn't exist, because $x^{4n-1}$ gets very large near $x=0$.
• Sketch:

MAT 2015 Q3

(i) There are lots of choices that work! To keep things simple, I picked constant functions $f(x)=\frac{1}{200}$ and $g(x)=0$. Then $|f(x)-g(x)|$ is less than $\frac{1}{100}$, but not less than $\frac{1}{320}$.

(ii) In this case, $f(x)-g(x)=\sin(4x^2)/400$. The $4x^2$ inside the brackets doesn't really matter; whatever the value of $\theta$, we have $|\sin(\theta)|<1$. So in this case we have\\ $|f(x)-g(x)|\leq 1/400$, which is less than $1/320$ for all $x$.

(iii) I can integrate for $\displaystyle g(x)=1+x+\frac{x^2}{2}+\frac{x^3}{6}+\frac{x^4}{24}$.

The value of $|g(x)-f(x)|$ is $x^4/24$, but that can only be as large as $(1/2)^4 / 24$, and that's less than $1/320$.

(iv) I'd like something involving $h(x)$ and $g(x)$, so that they appear on opposite sides of the equation. I'll take the difference between the defining equations for $h(x)$ and $g(x)$ for $$h(x)-g(x)=1-1+\int_0^x h(t)\,\mathrm{d}t - \int_0^x f(t)\,\mathrm{d}t.$$ This rearranges to the target expression, if I subtract $f(x)$ from both sides.

(v) There's a given range for $x$. The largest value of the integral would come if, hypothetically, $x=\frac{1}{2}$ and if $h(t)-f(t)$ were equal to its maximum value of $h(x_0)-f(x_0)$ all the way from $t=0$ to $t=\frac{1}{2}$. That would give an area of $\frac{1}{2}\times (h(x_0)-f(x_0))$.

(vi) We've been told that $h(x)\geq f(x)$, so $h(x)-f(x)\geq 0$. We just need to check that $h(x)-f(x)\leq 1/100$. It's enough to check that the maximum value $h(x_0)-f(x_0)$ is less than $1/100$.

In part (v) we worked out a fact about the integral in part (iv). Together, we have $$h(x)-f(x)\leq g(x)-f(x)+\frac{1}{2}\left(h(x_0)-f(x_0)\right).$$

But if we set $x=x_0$ and rearrange, this shows that $\frac{1}{2}\left(h(x_0)-f(x_0)\right)\leq g(x_0)-f(x_0)$. And we know from part (iii) that the last expression there is less than $1/320$. So the expression $h(x_0)-f(x_0)$ is less than $1/100$ and we have a good approximation.

Extension

• If $h(t)=e^t$ then the right-hand side is $1+\int_0^x e^t\,\mathrm{d}t=1+\left[e^t\right]_0^x=e^x.$
• Perhaps we could try $h(x)=A e^{kx}$. Then the right-hand side becomes
  $$2+\int_0^x 3 Ae^{kt}\,\mathrm{d}t=2+\left[\frac{3Ae^{kt}}{k}\right]_0^x=2+\frac{3A}{k}\left(e^{kx}-1\right).$$
  If $k=3$ and $A=2$ then this simplifies to $2e^{3x}$ which is $h(x)$.
  So $h(x)=2e^{3x}$ is a solution.