Trigonometry

Part of the Oxford MAT Livestream.

Solutions are available here.

MAT syllabus

Solution of simple trigonometric equations. The identities
\begin{equation*}
\tan x = \frac{\sin x}{\cos x} ,\quad \sin^2 x + \cos^2 x = 1, \quad \sin\left(90^\circ - x\right) = \cos x.
\end{equation*}
Periodicity of sine, cosine and tangent. Sine and cosine rules for triangles.

Revision

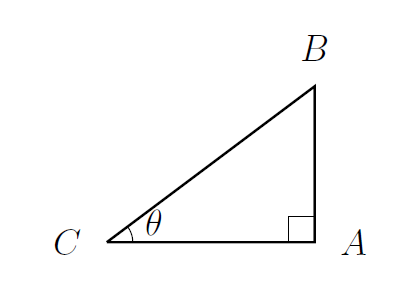
• If triangle $ABC$ is right-angled at $A$ and $\angle BCA=\theta$, then we define $$\sin\theta=\frac{|AB|}{|BC|}, \qquad \cos \theta=\frac{|AC|}{|BC|},\qquad \tan\theta=\frac{|AB|}{|AC|}.$$
• So $\displaystyle \tan\theta=\frac{\sin\theta}{\cos\theta}$.
• Pythagoras' Theorem states that $|AB|^2+|AC|^2=|BC|^2$ so $\sin^2\theta+\cos^2\theta=1$.
  It follows that $-1\leq \sin \theta \leq 1$ and $-1\leq \cos \theta \leq 1$.
• Since the angles in a triangle add up to $180^\circ$, the angle at $B$ is $90^\circ-\theta$.
  Looking at the triangle that way around, we can deduce that $\sin(90^\circ-\theta)=\cos\theta$ and $\cos(90^\circ-\theta)=\sin\theta$.
• The sine, cosine, and tangent functions are all periodic; $$\sin(x+360^\circ)=\sin x, \qquad \cos(x+360^\circ)=\cos x,\qquad \tan (x+180^\circ)=\tan x.$$
• Also, we have $\sin (-x)=-\sin x$, and $\cos(-x)=\cos(x)$.

Now consider a triangle that is not necessarily right-angled.

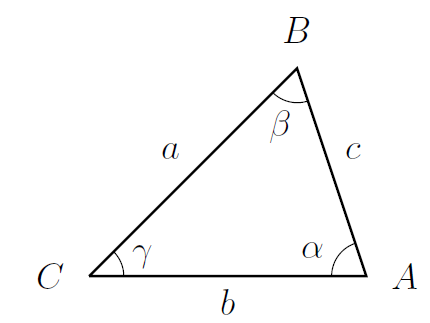
Let's write the angles at $A$, $B$, $C$ as $\alpha$, $\beta$, $\gamma$ respectively, and call the side-lengths $a=|BC|$, $b=|AC|$, $c=|AB|$.

• The area of this triangle is $\displaystyle \frac{1}{2}ab\sin\gamma=\frac{1}{2}bc\sin \alpha=\frac{1}{2}ca\sin\beta$.
• (The cosine rule) We have $a^2=b^2+c^2-2bc\cos\alpha$.
• (The sine rule) We have $\displaystyle \frac{\sin \alpha}{a} = \frac{\sin \beta }{b} = \frac{\sin \gamma}{c}$.

Revision Questions

1. Find the area of an equilateral triangle with all three sides of length $a$.
2. Find all the solutions to $\displaystyle \sin x = \frac{1}{2}$ with $0\leq x < 360^\circ$.
3. Find all the solutions to $\tan x = 1$ with $0\leq x < 360^\circ$.
4. Find all the solutions to $\tan (45x) = 1$ with $0\leq x < 360^\circ$.
5. A triangle has angles $30^\circ$, $60^\circ$, and $90^\circ$ and has side lengths $1$, $\sqrt{3}$, and $2$. Write down three expressions for the area using the three formulas above, and check that they all give the same value.
6. Write $(\cos x + \sin x)^2$ in terms of the variable $u=\cos x \sin x$.
7. For $0\leq x<90^\circ$, write $1-\sin^2 x+\sin^4 x-\sin^6 x+\dots$ as a single expression (not an infinite sum) in terms of $\cos x$. Why have I excluded $90^\circ$ from the range here?
8. Write $\cos^4x+\cos^2x$ in terms of $\sin x$.
9. Simplify $\cos(450^{\circ} -x)$.
10. Simplify $\cos(90^\circ-x)\sin (180^\circ-x)-\sin(90^\circ-x)\cos(180^\circ -x)$.
    (If you know a fact about $\sin(A-B)$, you may only use it here if you prove it!)
11. A triangle $ABC$ has side lengths $AB=3$ and $BC=2$, and the angle $\angle ABC=120^\circ$. Find the remaining side length $AC$, the area of the triangle, and an expression for $\sin \angle BCA$.
12. From the cosine rule, and the fact that $-1\leq \cos \alpha\leq 1$, deduce that for any triangle with side lengths $a>b>c>0$, we must have $a<b+c$ (this is the rule that "the longest side is shorter than the sum of the other two sides" or said differently "the shortest route from $B$ to $C$ is a straight line" also known as "the triangle inequality").
13. A triangle has side lengths 8, 13, and 15. Find the exact value of one of the angles in degrees.

MAT questions

MAT 2014 Q1E

As $x$ varies over the real numbers, the largest value taken by the function $$\left( 4\sin ^{2}x+4\cos x+1\right) ^{2}$$ equals
(a) $17+12\sqrt{2}$,
(b) $36$,
(c) $48\sqrt{2}$,
(d) $64-12\sqrt{3}$,
(e) $81$.
 

Hints

• This question involves both $\cos x$ and $\sin x$. Can you simplify by replacing one with the other?
• Watch out for the power of two on the outermost brackets. A very negative or a very positive value inside the brackets would give us a large value overall, after squaring.
• Don't multiply out the square though, it's easier to first think about the values taken by the function inside the brackets, and then work out what happens when those values are squared.

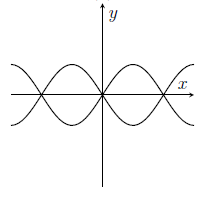
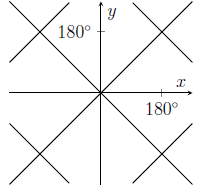
MAT 2015 Q1G

The graph of $\cos^2(x) = \cos^2(y)$ is sketched in

(a)

(b)

(c)

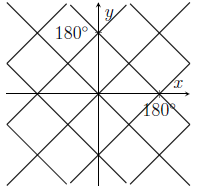
(d)

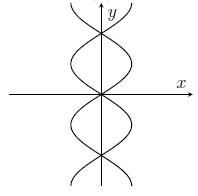
(e)

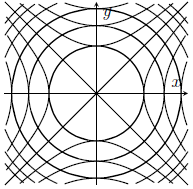
Hints

• We need to find all the ways in which $x$ and $y$ could give the same value of $\cos^2$. If $x$ and $y$ are equal, then $\cos^2 x=\cos^2 y$. But there are other cases to consider.
• Can you think of any symmetries or transformations that could help you find inputs that give the same value of $\cos^2$?
• These other cases might lead to other relationships between $x$ and $y$. We would like to plot all of these cases on the same axes.

MAT 2016 Q1D

How many solutions does $ \cos^n(x) + \cos^{2n}(x) = 0$ have in the range $0 \leqslant x \leqslant 2\pi$ for an integer $n \geqslant 1$?

(a) 1 for all $n$,
(b) 2 for all $n$,
(c) 3 for all $n$,
(d) 2 for even $n$ and 3 for odd $n$,
(e) 3 for even $n$ and 2 for odd $n$.

Hints

• Remember that $\cos^n(x)$ means $(\cos x)^n$ and $\cos^{2n}(x)$ means $(\cos x)^{2n}$. The substitution $u=(\cos x)^n$ might be helpful.
• The equation $u+u^2=0$ has solutions $u=0$ and $u=-1$. But how many values of $x$ are there for each of these cases?

MAT 2007 Q4 (modified)

In the diagram below is sketched the circle with centre $\left(1,1\right) $ and radius $1$ and a line $L$. The line $L$ is tangential to the circle at $Q$; further $L$ meets the $y$-axis at $R$ and the $x$-axis at $P$ in such a way that the angle $OPQ$ equals $\theta $ where $0<\theta <90^\circ$.

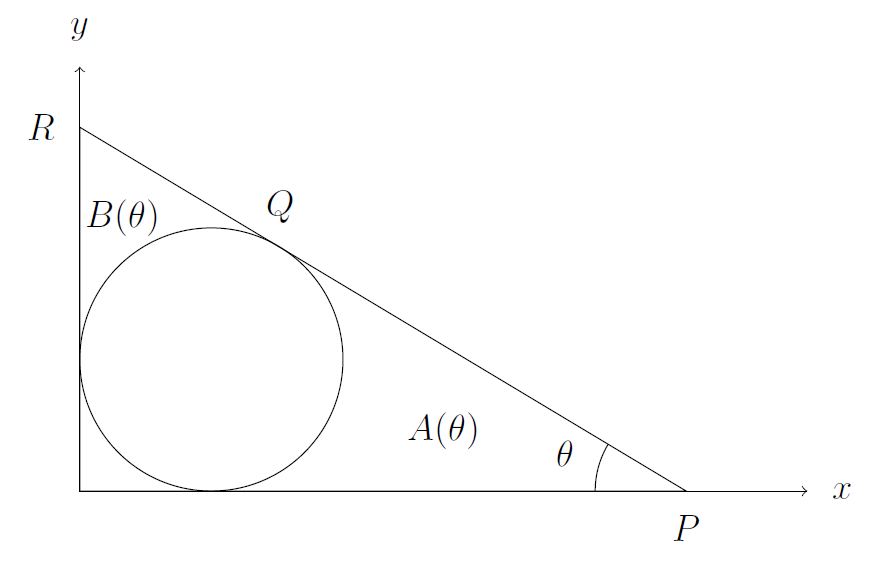
(i) Show that the co-ordinates of $Q$ are
\begin{equation*}
\left( 1+\sin \theta ,1+\cos \theta \right),
\end{equation*}
and that the gradient of $PQR$ is $-\tan \theta$.

Write down the equation of the line $PQR$ and so find the co-ordinates of $P$.

(ii) The region bounded by the circle, the $x$-axis and $PQ$ has area $A\left( \theta \right) $; the region bounded by the circle, the $y$-axis and $QR$ has area $B\left( \theta \right) $.

Explain why $A\left( \theta \right) =B\left( 90^\circ-\theta \right)$ for any $\theta $.

Calculate $A\left( 45^\circ \right) .$

(iii) Show that
\begin{equation*}
A\left( 60^\circ \right) =\sqrt{3}-\frac{\pi }{3}.
\end{equation*}

Hints

(i) Join $Q$ to the centre of the circle. What are the coordinates of the centre of the circle? If you could magically determine the size of one angle in order to determine the coordinates of $Q$ relative to te centre of the circle, which angle would you want to determine? To find this angle, imagine cases where $\theta$ is small or large and imagine the effect on your angle. That might give you an idea about the way your angle depends on $\theta$. Try to prove the relationship with trigonometry (identify a triangle which includes information you know and information you want).

(ii) Draw separate pictures with $\theta$ and with $90^\circ-\theta$. Label your diagrams carefully, being sure not to go too fast and accidentally label the picture with what you want to be true rather than what you know to be true.

For $A(45^\circ)$, the result $A(\theta)=B(90^\circ-\theta)$ might be helpful. You might like to draw a new diagram in this special case. It might help to draw lines joining the centre of the circle to the $x$-axis and/or to the $y$-axis and/or to $P$ and/or to $R$. Remember that you know the coordinates of $P$.

(iii) This time, I would draw one more diagram. I can't see a way to use the fact that $A(\theta)=B(90^\circ-\theta)$. But I can spot some right-angled triangles, and I know quite a few distances.

The expression I'm aiming for reminds me of calculations from the previous sheet.

Extension

[Just for fun, not part of the MAT question]

• Find $A(\theta)$ in terms of $\theta$. Sketch the graph of $A(\theta)$ for $0<\theta<90^\circ$.

MAT 2012 Q4 (modified)

The diagram below shows the parabola $y=x^{2}$ and a circle with centre $(0,2)$ just "resting" on the parabola. By "resting" we mean that the circle and parabola are tangential to each other at the points $A$ and $B$. $A$ is in the region $x<0$ and $B$ is in the region $x>0$.

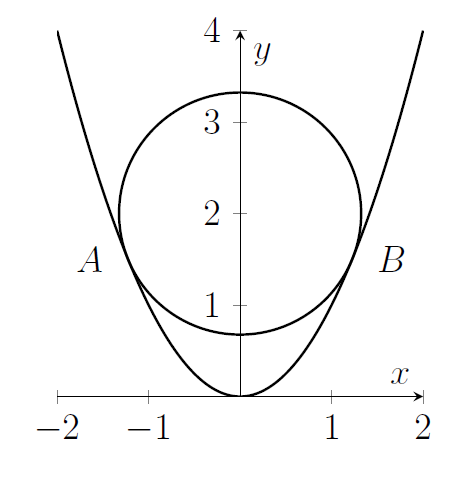
(i) Let $(x,y)$ be a point on the parabola such that $x\neq 0$. Show that the gradient of the line joining this point to the centre of the circle is given by
\begin{equation*}
\frac{x^{2}-2}{x}.
\end{equation*}

(ii) With the help of the result from part (i), or otherwise, show that the coordinates of $B$ are given by
\begin{equation*}
\left( \sqrt{\frac{3}{2}}~,~\frac{3}{2}\right) .
\end{equation*}

(iii) Show that the area of the sector of the circle enclosed by the radius to $A$, the minor arc $AB$ and the radius to $B$ is equal to 
\begin{equation*}
\frac{7\pi}{4}\cos ^{-1}\left( \frac{1}{\sqrt{7}}\right) \frac{1}{180^\circ} \quad \text{or, equivalently,}\quad     \frac{7\pi}{8}\cos ^{-1}\left( -\frac{5}{7}\right) \frac{1}{180^\circ}.
\end{equation*}
[$\cos^{-1} x$ is the angle $\alpha$ in degrees such that $\cos \alpha=x$, and such that $0\leq \alpha\leq 180^\circ$.]

(iv) Suppose now that a circle with centre $(0,a)$ is resting on the parabola, where $a>0$. Find the range of values of $a$ for which the circle and parabola touch at two distinct points.

(v) Let $r$ be the radius of a circle with centre $(0,a)$ that is resting on the parabola. Express $a$ as a function of $r$, distinguishing between the cases in which the circle is, and is not, in contact with the vertex of the parabola.

Hints

(i) The gradient is the change in $y$ divided by the change in $x$.

(ii) Recall that the radius is at right angles to the tangent for a circle. And it's a shared tangent! We'll need to know the gradient of the parabola at $B$, and the gradient of the tangent to the circle at $B$. That second one seems very complicated until you remember a fact about circles.

(iii) We've got two equivalent expressions that we could aim for. You might like to draw a diagram and aim for an angle, because once we have an angle it's relatively easy to find the area of a sector. Along the way, we'll probably need to find the radius of the circle, we haven't actually worked that you yet.

(iv) Repeat the calculation from parts (i) and (ii) but with $(0,a)$ instead of $(0,2)$ for the centre of the circle. When can we solve for the point $B$?

(v) We had to work out the number $\sqrt{7}/4$ as part of the calculation above; let's aim to generalise this. Check your general answer by setting $a=2$ to make sure that you get the same number that you got before.

Separately, think about the case where the origin is the point of contact. The expression for $r$ is nice and simple in this case.

Extension

[Just for fun, not part of the MAT question]

• You're given that $\cos 2\theta=2\cos^2\theta-1$ for all $\theta$. Suppose that $\cos \theta=1/\sqrt{7}$. Find $\cos 2\theta$. Interpret the two different expressions in part (iv).
• Compare your working with the question about closest points on the Algebra sheet (MAT 2009 Q4).