MAT syllabus practice solutions

updated July 2020 (first version October 2019)

- James Munro, Admissions Coordinator for Maths at Oxford.
Comments or corrections should be sent to james.munro [at] maths.ox.ac.uk

These are the solutions to the MAT syllabus practice questions.

Solve $x^2-x-1=0$
The quadratic formula gives $x=\frac{1\pm\sqrt{5}}{2}$.
Solve $x^4-x^2-1=0$
Write $y=x^2$ to get a quadratic for $y$. This is the quadratic above for $y$, so $x^2=\frac{1\pm\sqrt{5}}{2}$. But $x^2\geq0$ so $x=\pm\sqrt{\frac{1+\sqrt{5}}{2}}$.
Write $x^2+4x+3$ in the form $(x+a)^2+b$
$(x+2)^2-1$
How many real solutions does $x^2+bx+1=0$ have? Find the different cases in terms of $b$.
The discriminant, $b^2-4$, is positive if $b>2$ or $b<-2$, negative if $-2<b<2$ and zero if $b=\pm2$. So there are two real solutions if $b>2$ or if $b<-2$, one real solution if $b=\pm2$ and no real solutions otherwise.
Factorise $x^2+4x+3$
$(x+1)(x+3)$
Let $p(x)=x^3-13x^2-65x-51$. Check that $p(17)=0$. Factorise $p(x)$.
$p(17)=17^3-13\times17^2-65\times17-51=17\left(17^2-13\times 17-65-3\right)=17^2\left(17-13-4\right)=0$. So $(x-17)$ is a factor. Polynomial division gives $p(x)=(x-17)(x^2+4x+3)$, so $p(x)=(x-17)(x+1)(x+3)$.

Solve the simultaneous equations $x+y=1$ and $x-y=3$.
$x=2$ and $y=-1$.
For which values of $x$ is it true that $x^2+4x+3>0$?
$x>-1$ or $x<-3$.
Expand $(2x+3)^3$
$8x^3+36 x^2+54x+27$
I've got four playing cards; the ace and king of clubs, and the ace and king of hearts. I shuffle the cards together and deal them out left to right. What's the probability that the kings and aces alternate? (they alternate if they are either arranged as $AKAK$ or $KAKA$)
There are 24 possible orders for the cards. Eight of these have alternating kings and aces, so the probability is 1/3.

Differentiate $x^{17}$ with respect to $x$.
$17x^{16}$
Differentiate $\sqrt{x}$ with respect to $x$.
$\frac{1}{2\sqrt{x}}$
Differentiate $e^{3x}$ with respect to $x$.
$3e^{3x}$
Differentiate $2e^{-x}-x^2$ with respect to $x$.
$-2e^{-x}-2x$
Find the tangent to the curve $y=e^x+1$ at $x=2$.
$y=e^2(x-2)+e^2+1$
Find the normal to the parabola $y=x^2$ at $x=3$.
$y=-\frac{1}{6}(x-3)+9$
Find the turning points of the curve $y=x^4-2x^3+x^2$. Identify whether the turning points are maxima or minima.
Turning points at $x=0$ (minimum), $x=\frac{1}{2}$ (maximum), $x=1$ (minimum).
For which values of $x$ is $y=x^4-2x^3+x^2$ increasing? For which values of $x$ is it decreasing?
Increasing for $0<x<\frac{1}{2}$ and for $1<x$. Decreasing for $x<0$ and for $\frac{1}{2}<x<1$.
Two points $A$ and $B$ are on the curve $y=x^3+x^2+x+1$. $A$ is held fixed at $(1,4)$. The point $B$ is moved along the curve towards $A$. What happens to the line through $A$ and $B$?
The tangent at $A$ is $y=6x-2$. If the line $AB$ has equation $y=mx+c$ say, then $m$ gets closer and closer to 6 and $c$ gets closer and closer to $-2$.

Suppose that the derivative of a polynomial $p(x)$ with respect to $x$ is $q(x)$. Find $\displaystyle \int q(x)\,\mathrm{d}x$.
$p(x)+c$ where $c$ is a constant
Find the area enclosed by the polynomial $x^2+4x+3=0$ and the $x$-axis.
$\frac{4}{3}$
Find $\displaystyle \int_{-1}^1 1+x+x^2+x^3+x^4+x^5+x^6\,\mathrm{d}x$
Note that $\int_{-1}^1 x^a \,\mathrm{d}x=0$ for $a$ odd. The integral is 2$\left(1+\frac{1}{3}+\frac{1}{5}+\frac{1}{7}\right)=\frac{352}{105}$.

Sketch graphs of
$$y=x^2+4x+3,\quad y=x^3+4x^2+3x,\quad y=2^x, \quad y=\log_2 x$$ on separate axes.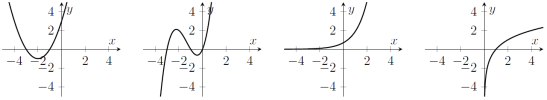
Sketch graphs of $y=\sin x$, $y=\cos x$ and $y=\tan x$ on the same axes.

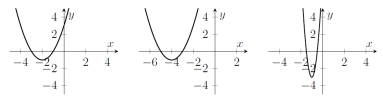
Let $f(x)=x^2+4x+3$. If you didn't sketch a graph of this before, sketch one now.
Sketch a graph of $y=f(x+2)$.
Sketch a graph of $y=3 f( 2 x)$.

Add the vectors $\displaystyle \left(\begin{matrix}1\\2\end{matrix}\right)$ and $\displaystyle \left(\begin{matrix}3\\-2\end{matrix}\right)$.
$\displaystyle \left(\begin{matrix}
4\\0
\end{matrix}\right)$
Find the equation of the line through $(1,0)$ and $(0,-1)$.
$y=x-1$
Find the equation of the line through $(1,2)$ with gradient 3.
$y=3(x-1)+2=3x-1$
A circle has centre $(-1,4)$ and radius 3. Write down an equation for the circle.
$(x+1)^2+(y-4)^2=9$
What's the area of this circle?
$9\pi$
Points $A$ and $B$ lie on a circle with centre $O$ and radius 1. The angle $\angle AOB$ is 120$^\circ$. Find the length of the arc between $A$ and $B$. Find the area enclosed by that arc and the radii $OA$ and $OB$.
It's a third of a circle, so the arc length is $2\pi/3$ and the area is $\pi/3$.

Solve $\sin x = \frac{1}{2}$.
$x=30^\circ+n\times 360^\circ$, or $x=150^\circ+n\times 360^\circ$, for any whole number $n$.
Solve $\tan x = 1$.
$x=45^\circ+n\times 180^\circ$ for any whole number $n$
Write $\cos^4x+\cos^2x$ in terms of $\sin x$.
$(1-\sin^2x)^2+(1-\sin^2 x)=2-3\sin^2x+\sin^4x$.
Simplify $\cos(450^{\circ} -x)$
$\sin x$
A triangle $ABC$ has side lengths $AB=3$ and $BC=2$, and the angle $\angle ABC=120^\circ$. Find the remaining side length $AC$, the area of the triangle, and an expression for $\sin \angle BCA$.
Cosine rule; $AC=\sqrt{19}$. The area of the triangle is $3\sqrt{3}/2$. Sine rule; $\sin \angle BCA=(3\sqrt{3}/2\sqrt{19})$

A sequence is defined by $a_0=1$, $a_1=1$, $a_2=1$, and
$$a_n=a_{n-1}+a_{n-2}+a_{n-3}\quad\mbox{for $n\geq 3$.}$$
Find $a_{10}$.
$a_{3}=3$, $a_4=5$, $a_5=9$, $a_6=17$, $a_7=31$, $a_8=57$, $a_9=105$, $a_{10}=193$.
A sequence has first term 3 and each subsequent term is 5 more than the previous term. Find the sum of the first four terms.
$4\times 3+\frac{4\times 3}{2}\times 5=42$
A sequence has first term 4 and each subsequent term is 6 times more than the previous term. Find the sum of the first four terms.
$4\left(1+6+6^2+6^3\right)=4\frac{6^4-1}{6-1}=4\frac{1295}{5}=4\times 259=1036$.
When does the sum $1+x^3+x^6+x^9+x^{12}+...$ converge? Simplify it in the case that it converges.
Converges when $-1<x<1$. In that case, it converges to $1/(1-x^3)$.

For more MAT resources, see the MAT page.