Busbridge lecture
For a brief (and not up-to-date) account of our history here is the text of a lecture by the late I. W. Busbridge, who was a fellow of St Hugh's College from 1945 to 1970. It is reproduced here without revision.
Foreword
The following account of mathematics at Oxford was first given as my presidential address to the Invariant Society in 1961 and I have repeated it three times at the request of the Society, each time making modifications resulting from further reading. At no time had I any thought of publication and I kept no detailed account of the exact sources of my information. My greatest debt is to R.T. Gunther's Early Science in Oxford and to C.E. Mallet's History of the University of Oxford and I may have quoted many times from either of these hooks. Most of my sources of information are listed in the Bibliography at the end, but I have not included newspaper cuttings, official obituary notices and the Dictionary of National Biography. In preparing my lecture for publication, I have only inserted a reference to the Bibliography when my source of information is unusual or where I know that I am quoting.
My lecture was always fluid when I reached the 20th Century and I just talked to my audience according to the time available. I have had to write this part of the lecture and I have inserted quite a lot that I never said!
I am greatly indebted to the Oxford Mathematical Society for making the publication of my lecture possible.
I.W.B., August 1974.
OXFORD MATHEMATICS AND MATHEMATICIANS
I
Long before Isaac Newton made Cambridge a world-famous centre for mathematics, mathematicians in Oxford were producing work of outstanding merit. Since mediaeval days there have been eminent mathematicians who have attracted pupils to Oxford and made the School of Mathematics one of outstanding quality. There have also been periods of stagnation during which mathematical studies degenerated to routine learning or worse.
The University course, from its foundation until about 1550, was based on the Seven Liberal Arts. These were divided into
- The Trivium: Grammar, Rhetoric, Dialectic;
- The Quadrivium: Music, Arithmetic, Geometry, Astronomy.
A student studied the Trivium for four years and the Quadrivium for three. The main purpose of arithmetic was the calculation of the date of Easter, and astronomy was closely allied to astrology. Geometry included geography and a little Euclid, and even as late as 1550 few students progressed beyond the fifth proposition of Euclid, Book 1:
The angles at the base of an isosceles triangle are equal.
This is the so-called pons asinorum.
Until the end of the 17th century at least, a mathematician was also am astronomer, a philosopher, and probably a theologian, and even a physician as well. Not infrequently a well-known mathematician ended his life as a bishop or even as an archbishop. In writing about the early mathematicians I shall treat observational and computational astronomy as part of mathematics.
II
1200-1600
The first mediaeval Oxford mathematician of note was John of Holywood or John de Sacro Bosco, as he was usually called. He died in 1244. He was educated at Oxford but subsequently moved to Paris and taught there. His best known books are De Algorithmo (or the art of computing in the decimal system), De Computo Ecclesiastio, De Astrolabio and De Sphaera Mundi. The latter was a best-seller for over 200 years and as late as 1384 it appeared on a list of books to he read for the degree of B.A. at the University of Prague.
Two other early Oxford philosophers must be mentioned: Robert Grosseteste (ca 1168-1253), Bishop of Lincoln, and Roger Bacon (ca 1214-1294). Modern research is beginning to elevate Grosseteste above Bacon as an original thinker. He was the real founder of the tradition of scientific thought in mediaeval Oxford. The theory of science was based on Aristotle's distinction between knowledge of a fact and knowledge of the reason for the fact. There were three essential aspects in scientific theory: the inductive, the experimental and the mathematical. Mathematics alone could not provide an adequate description of a phenomenon. For example, geometry could give an account of an optical phenomenon, but it could not explain why it happened.
Both Grosseteste and Bacon gave particular importance to the study of optics and both attempted to explain the rainbow. Both asserted that the propagation of light was not a flow like water, but a kind of pulse as in sound. Bacon noted, however, that light travelled much faster than sound, for if someone at a distance is banging with a hammer, we see the blow before we hear the sound.
Bacon's life story is well-known. He came up to Oxford at an early age and took holy orders at the age of 19 years. Soon after this he went to Paris for about six years, studying and lecturing there. He returned to Oxford and taught in the University until about 1253 and it was during this time that he must have come under the influence of Grosseteste. He spent most of his money on scientific MSS from Arab sources and scientific instruments, and he wrote on scientific problems in his spare time. He entered the Franciscan order in 1257 and he was forbidden by his superior to lecture on or to publish scientific work. Clement IV, who became Pope in 1265, had heard of Bacon's work during a visit to England and, by a papal mandate of 22 June 1266, he ordered Bacon to send him a copy of his philosophical writings. Fifteen months later Bacon sent Clement his Opus Maius followed in 1268 by his Opus Minus and Opus Tertium, which contained resumes, corrections and additions. Unfortunately Clement died in 1268. In 1278 Bacon's opinions were condemned and in 1280 he was imprisoned for life. He was released about a year before his death in 1294.
Bacon argued for the usefulness of mathematics in almost every realm of academic activity and he called mathematics `the first of the sciences', 'the alphabet of philosophy', and `the door and key of the sciences', but apart from trivial results in practical contexts such as mechanics, optics and astronomy, he made no real contribution to the advancement of the subject. His contributions to science were much more substantial. He is thought to have discovered the principle of the telescope and he wrote with great insight on calendar reform.
In the 14th Century the so-called Merton School made Oxford famous for its mathematics and astronomy. The better known members of the Merton School were
- Thomas Bradwardine, 1290-1349,
- Richard of Wallingford, ca 1292-1336,
- John Maundith, Elected a fellow 1305, Bursar 1311,
- Simon Bredon, ca 1300-1372,
- John Ashenden, Elected a fellow 1338,
- Wm. Rede, 1325-1385.
Simon Bredon migrated to Merton from Balliol. Wm. Rede built the Merton Library.
Merton had been founded in the 13th Century with the purpose of leaving its fellows free to pursue their studies in the natural sciences unencumbered with liturgical obligations. Within 100 years Merton attained a pre-eminence in scientific studies that placed it well ahead of any other comparable foundation in Europe. There were no truly English astronomical tables and the construction of accurate tables for the meridian of Oxford was undertaken. John Maundith and Wm. Rede were the two who were principally concerned with the tables. Copies of these still exist.
Thomas Bradwardine is considered to be the greatest English mathematician of the 14th Century. He did notable work on the sums of angles in star polygons and in the theory of proportion (10). So learned were his discourses (theological, philosophical and mathematical) that he became known as Dr. Profundus. He became Archbishop of Canterbury and Chaucer classed him with St. Augustine.
Richard of Wallingford was the son of a skilful blacksmith of Wallingford and we have details of some of his inventions. Later in life he became Abbot of St. Albans and in about 1320 constructed an astronomical clock for the Abbey which was in advance of any other in Europe. It showed the motions of the sun, moon and stars, with the ebb and flow of the tides. He left a handbook (still in existence) explaining its use.
Until recently very little was known about the Merton School. The reason is as follows: In 1549 there were Royal Commissions on Oxford and Cambridge under Edward VI. The Visitors to Oxford ordered a large number of books from the Merton Library to be burned or sold as waste paper. A cartload of valuable MSS is said to have been taken away. Thomas Allen (1542-1632) of Gloucester Hall, who was the best Oxford mathematician in the second half of the 16th Century, collected MSS of the Merton School (evidently ones sold for waste paper!) and ultimately these came to the Bodleian Library. These are now being studied by Dr J.D. North (Merton) who expects to bring out a critical edition of the works of Richard of Wallingford [see also refs. 10 and 15].
In the 15th Century Oxford produced two famous mathematicians: Cuthbert Tonstall (1474-1559, Balliol) and Robert Recorde (1510-1558, Fellow of All Souls). Both migrated to Cambridge and they can be regarded as the founders of the Cambridge Mathematical School, as they are the first mathematicians at Cambridge of whose lives and works any details are known. The more famous of the two is Robert Recorde. So eloquent was he as a lecturer that he was rewarded by the applause of his audience!
Recorde was an educationalist and he wrote school textbooks in English. His Arithmetic, Geometry and Algebra are
- Grounde of Artes (1542)
- Pathway to Knowledge (1551),
- Whetstone of Witte (1557).
The first two ran to many editions. In Grounde of Artes the rules of arithmetic were explained so simply that `euerie child can do it'. Multiplication involved only multipliers up to 5 and was done as shown below for 8 times 7 and x times y

The book is set out in the form of a dialogue between master and pupil. After the section on multiplication we have
'Scholar. Syr, what is the chiefe use of Multiplication?
Mayster. The use of it is greater than you can yet understand.'
There is a copy (first edition) of Whetstone of Witte in the library of The Queen's College. This is `Arithmetic part II and Algebra' and it was the first English algebra book. The earliest use of the word `algebra' occurs in Recorde's Pathway to Knowledge. In Whetstone of Witte the `equals sign' occurs for the first time. Recorde asks what can be more equal than two parallel lines of the same length and he therefore uses ![]() (rather elongated!) in equations.
(rather elongated!) in equations.
After the departure of Recorde and Tonstall to Cambridge, Oxford mathematics sank to a low ebb. In 1549, as stated above, Royal Commissions on Oxford and Cambridge were appointed with comprehensive reforming powers. The Visitors brought with them a body of new Statutes drafted by the King's Council. These fixed the length of terms and vacations, the days and hours of public lectures and the authors to be studied. Mathematics was to be studied from 12 to 1 p.m. Moreover the young student from school was to devote his first year to mathematics.
But how could mathematics be studied without a teacher? In 1554 a group of Oxonians invited John Dee of St. John's College, Cambridge, to come and lecture in Oxford. He refused, but his pupil Thomas Digges of Queens' College, Cambridge, came instead. He was the first English author to describe the theodolite and he edited the works of his father, Leonard Digges (University College, Oxford), who was the first maker of efficient telescopes.
III
1600-1750
During the last half of the 16th Century the world was awakening to new ideas in science and mathematics. These are the dates of the outstanding mathematicians and astronomers of the period 1550-1650, but beginning with Copernicus.
| Copernicus | 1473-1543 |
| Napier | 1550-1617 |
| Briggs | 1561-1631 |
| Galileo | 1564-1642 |
| Kepler | 1571-1630 |
| Desargues | 1593-1662 |
| Descartes | 1596-1650 |
| Cavalieri | 1598-1647. |
Newton was born in 1642 and died in 1727.
It was due to the foresight of Henry Savile (1549- 1622) that Oxford played a major part in the development of the new learning. He was one of the most learned men of his day. He was a classical scholar and edited the works of St. Chrysostom in eight large volumes, but he was also something of a mathematician and astronomer. For 26 years he was Warden of Merton and for part of the time he was Provost of Eton as well. Towards the end of his life, deploring the wretched state of mathematical studies in England, he founded at Oxford in 1619 the Professorships of Geometry and Astronomy which still bear his name. He also bequeathed his library to the Bodleian `for the use chiefly of mathematical readers'.
One year earlier (1618) the Sedleian Professorship of Natural Philosophy was founded under the will of Sir Wm. Sedley, who left £2,000 to the University to be laid out in the purchase of land. This is now one of the mathematical chairs.
The statutes for the Savilian Chairs laid down that the professors were to be `persons of character and repute, well skilled in mathematics and 26 years of age'. They might be chosen from `any part of Christendom'. The statutes also laid down the books which were to be studied, of which the only modern author was Copernicus!
In 1614 Napier had discovered natural logarithms and in 1617 logarithms to the base 10 were published by Briggs. Savile chose Briggs as his first Professor of Geometry and Bainbridge as Professor of Astronomy. In addition to logarithms to the base 10, Briggs invented the common method of long division. He had the distinction of being the first holder of each of the two earliest chairs of mathematics to be founded in Britain: that at Gresham College in London (founded in 1596) and the Savilian Chair of Geometry (1619).
Edmund Gunter (1581-1626) of Christ Church was a candidate for the first Savilian Chair of Geometry. He was the inventor of the straight logarithmic scale (1620), calculations being made with the aid of compasses. (The slide-rule itself was invented by Oughtred about a year later.) He published tables of logarithms of sines and of tangents to 7 decimal places and the terms cosine, cotangent, cosecant and the notation log a are due to him. Henry Savile sent for Gunter who came `and brought with him his sector and quadrant and fell to resolving of triangles and doeing a great many fine things. Said the grave knight, "Doe you call this reading of Geometrie? This is shewing of tricks, man!"' [Quoted from ref (7). Gunther attributes it to Aubrey's Life of Savile.] And so he sent for Briggs.
The years following the foundation of the Savilian and Sedleian Chairs was a period of intellectual ferment. Mathematics was developing rapidly, and science, based on the philosophy of Sir Francis Bacon, was concerned to build up by experimentation a complete natural history, from which, it was expected, the primary laws of nature would be apparent.
During the Civil War, Oxford suffered three Visitations. The first Board of Visitors (appointed in 1647) replaced the royalist Savilian professors (Turner and Greaves) by John Wallis and Seth Ward. Both were men fired with the new learning. In the same year (1649) Christopher Wren entered Wadham as an undergraduate and the Oxford Philosophical Society was started in the lodgings of John Wilkins, Warden of Wadham. Wilkins was a man of vision and he even foresaw the possibility of space travel. I quote from (12):
`Writing on the physical nature of the moon, he had maintained that once man had mastered the art of flying, it would be "possible for some of our posterity to find out a conveyance to this other world". After examining some of the obstacles with extraordinary perception, he came to the conclusion that "It is not the bignesse of any thing in this kind, that can hinder its motion, if the motive faculty be answerable thereto. We see a great ship swimmes as well as a small corke, and an Eagle flies in the aire as well as a little gnat."'
Wilkins collected round him a brilliant group and they met weekly to discuss `Philosophicall Experiments'. By 1652 there were about thirty members, but the most constant in attendance were Wilkins himself, Seth Ward, Robert Boyle, Sir William Petty (anatomy), Matthew Wren (Christopher's cousin), Christopher Wren, John Wallis, and a few others. By 1658 many of the members of the Oxford Philosophical Society were back in London and after the Restoration in 1662 it was incorporated by Royal Charter as the Royal Society.
John Wallis (1616-1703) was educated at Queens' College, Cambridge, and he was Savilian Professor of Geometry for over 50 years. His mathematical work is notable partly for the introduction of the use of infinite series as an ordinary part of analysis, and partly for explaining the `modern mathematics', i.e. the analytical geometry of Descartes (published in 1637) and Cavalieri's method of indivisibles (the forerunner of calculus). His most important books were Treatise on Conic Sections (1655) and Arithmetica Infinitorum(1656). The first of these clarified the work of Descartes and the second systematised and greatly extended the methods of Descartes and Cavalieri. Arithmetica Infinitorum became the standard book on the subject and it would have been almost certainly studied by Newton. Wallis introduced fractional and negative indices and he obtained the formula for pi, which is still known by his name, viz.
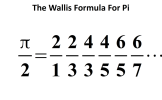
A third book, Algebra (1685), was the first to make systematic use of formulae.
In 1668 the problem of the collision of bodies was propounded by the Royal Society. Wallis, Wren and Huyghens sent in correct and similar solutions based on conservation of momentum, but Wallis considered imperfectly elastic bodies while the other two only dealt with elastic bodies.
Seth Ward (1617-59) was educated at Sidney Sussex College, Cambridge He lived in Oxford at the top of the tower in Wadham in a room which became known as the astronomy room. He did much to improve telescopes and published a theory of planetary motion. The difficulty of the `modern mathematics' is shown by the record that Seth Ward `did draw his geometricall schemes with black, red, yellow, green and blew inke to avoid the perplexity of A, B, C, etc.'. He ultimately became a bishop and was succeeded as Savilian Professor of Astronomy in 1661 by
Christopher Wren (1632-l723). He was Savilian Professor from 1661 to 1673 and he also occupied the astronomy room at Wadham. Had Wren not found his metier in architecture, he would have been better known as the brilliant mathematician and scientist that indeed he was. He excelled in geometrical demonstrations and Newton considered Wren, Wallis and Huyghens to be `beyond comparison the leading geometers of this age'. About 1656 Wren solved a problem proposed by Pascal to the geometers of England and retorted by sending a challenge to the French geometers. The challenge was unanswered, though Wren had himself solved the problem whioh had originally been issued by Kepler.
The Sheldonian Theatre was Wren's first large-scale building. It was started in 1664 and the official opening was in 1669. The magnificent painted ceiling, the work of Robert Streater, depicts (11) "Truth descending upon the Arts and Sciences". Theology, with her book with seven seals, is imploring the assistance of Truth in unfolding it. Truth is sitting on a cloud in the middle. On the opposite side of the circle from Theology are the mathematical sciences; Astronomy with the celestial globe bound about by the Milky Way, Geography with the terrestial globe, Arithmetic with a paper of figures, Optic with the perspective glass (telescope) Geometry with a pair of compasses on her left and a table with geometrical figures on it, and Architecture embracing the capital of a column.
It is not surprising that there was a reaction in some circles in Oxford against the new learning. After the official opening of the Sheldonian Theatre in 1669, Wallis wrote to Robert Boyle (4) describing the address given by the popular preacher and University Orator, Robert South, as follows:
`The first part ... consisted of satyrical invectives against Cromwell, the Royal Society and the new philosophy; the next of encomiastics in praise of the archbishop [Sheldon], the theatre, the vice-chancellor, the architect and the painter; the last of execrations against fanatics, conventicles, comprehension, and new philosophy, damning them ad infernos, ad gehennam.'
The Old Ashmolean (now the Museum of the History of Science), which adjoins the Sheldonian, was built by the master mason Thomas Wood between 1679 and 1683. In the basement was the first University chemistry laboratory, showing that the new philosophy was making progress.
Edmond Halley (1656-1742) was the last of the brilliant set of Oxford mathematicians and astronomers of this period. Like Wren he was a product of Oxford, being educated at Queen's, and it is difficult to say which of the two was the more versatile. Halley followed Wallis as Savilian Professor of Geometry (not Astronomy!), holding the chair from 1704 to 1742. He was Astronomer Royal (the second) from 1720 to 1742. The following list gives some idea of the range of his activities:
(i) As an undergraduate he managed to get himself and a friend a free passage to St. Helena to make observations of southern stars. On his return he was granted the degree of M.A. by a royal mandate of Charles II, who wrote as follows (13) to the Vice-Chancellor on November 18, 1678: "Having received a good account of the proficiency and learning of Edmond Halley of Queen's College and especially as to the mathematics and astronomy, whereof he has given good testimony by his observations during his abode in the island of St. Helena, recommending for the degree of M.A. without any condition of performing any previous or subsequent exercises for the same".
(ii) He was elected an F.R.S. at the age of 22 and was later Clerk and Secretary of the Royal Society.
(iii) He borrowed a ship from the Navy - and the Navy made him captain of it - which he successfully sailed across the Atlantic taking magnetic measurements. He went as far as lat. 52 degrees S. His papers on terrestrial magnetism are the best in that field for the next 300 years.
(iv) He predicted the return of his comet, and discovered the proper motion of the stars by comparing the positions of Arcturus and Sirius with the positions measured by Ptolemy.
(v) Appointed Astronomer Royal at the age of 65, he chose as his main task the observation of the moon for a period of 18 years and he completed his task.
(vi) He was the pioneer of all insurance tables of the expectation of life.
(vii) He collected information about trade winds, aurora and meteorites.
(viii) He corrected classical texts and investigated the place of landing of Julius Caesar in Britain.
(ix) Last, and far from least, he persuaded Newton to write the Principia and paid for the publication out of his own pocket. Here I quote from the Halley Lecture given by Prof. H. Dingle on the occasion of the tercentenary of Halley's birth (6).
`We cannot doubt that without Halley there would have been no Principia. To quote de Morgan, "but for him, in all human probability, that work would not have been thought of, nor when thought of written, nor when written printed ..." Details must be forgone. I can only say that in the year 1684, when Halley was 27, the question agitating the minds of the mathematically inclined members of the Royal Society was whether Kepler's laws required an inverse square law of gravitation; several had guessed that this must be so, but no-one was known to have proved it. Four years earlier Hooke had tried to draw Newton out on the subject, and had been snubbed for his pains. Halley at once went to Cambridge, invaded the cherished privacy of Newton who was half as old again as himself, and learned that Newton had solved the problem long before but had mislaid the papers. Realising the overwhelming importance of the question, Halley repeated his visit, wheedled Newton into repeating his proof and developing its implications, and received from him the first Book of his immortal volume in 1686. The Royal Society agreed to print it, but later appeared to regret the expense. Halley, who seems to have been alone in perceiving that all the money in the Mint was negligible compared with the value of Newton's work, offered without argument to pay for it himself. Two further Books followed, and Halley accepted the cost of printing these also. The whole work was published about mid-summer, 1687, with an untypically generous tribute from Newton to Halley in the Preface and a eulogy of Newton in Latin hexameters by Halley.'
It must be apparent from this list of Halley's activities, that he must have been absent from Oxford for considerable periods. If mathematical studies at Oxford were entirely dependent on the Savilian Professor of Geometry, then there often were no lectures!
IV
1750-1900
During the century following the death of Halley, when Cambridge mathematics was in the ascendant, there were no Oxford mathematicians of the first rank. [James Bradley (1692-1762) was an astronomer of the first rank whose life just overlaps this period. He was made Savilian Professor of Geometry in 1721 and was Astronomer Royal following Halley. He was the first astronomer to make the art of observing part of a methodical science.] Professors lectured less and less and the examinations for the B.A. and M.A. became more and more perfunctory. Moreover a man could not graduate in mathematics until he had graduated in classical subjects. At Cambridge, on the other hand, a man could not, until ahcut 1850, graduate in classics until he had graduated in mathematics. This, I believe, was the origin of the myth, which still persists, that Cambridge is the place for mathematics and science, and Oxford for classics and arts. The point is illustrated by the following story from Cambridge.
A classic, who was weak at mathematics, went to a coach. He asked him to choose twenty propositions of Euclid likely to be set so that he could learn them by heart. Later the number was reduced to ten. After the examination the delighted undergraduate went to the coach's room and said `I am through; I got eight of the propositions you chose and got them right to a comma'. As an afterthought he added `I am not sure that I put the right letters at the right corners, but I suppose that does not matter'.
At both universities the method of examination had been by disputation from mediaeval times, but reforms at Oxford began in about 1820 and parts of the examination began to be written. The effect was to empty the lecture rooms of the professors, for the college fellows did the examining and the lectures given by the professors were usually quite irrelevant. It was prudent to stick closely to what your college tutor considered to be necessary!
At this point something must be said about science teaching at Oxford [For further details see ref (14)]. In mediaeval days Medicine was one of the principal faculties, but from the 16th Century the College of Physicians had the right of licensing medical practioners and medical teaching practically lapsed at Oxford and Cambridge. There was always a School of Astronomy at Oxford, but the Savilian professor had only Halley's Observatory, still to be seen in New College Lane. In 1772 the building of the Radcliffe Observatory was started and for about 65 years the Savilian professor and the Radcliffe observer were one and the same person, but in 1839 the Radcliffe Trustees and the University authorities fell out, and the two offices were separated, leaving the Savilian professor only with Halley's observatory.
By 1800-1850 there were professors in most of the principal sciences, though one man often occupied two or even three chairs! As far as practical work is concerned, there was the Physick Garden (or Botanical Garden) opposite Hagdalen, which dates from 1622, and the Old Ashmolean (1683) which was the first public museum and laboratory in England. With the increasing interest in science in the first half of the 19th Century, colleges began to build their own laboratories in order to give their undergraduates practical instruction. From about 1835 onward there was constant agitation for more provision for science teaching, and finally, in 1849, degrees in science were established. But scientists still had to concentrate on classical subjects for Responsions and the First Public Examination. And in the 1852 syllabus for the Honour School of Natural Science it says
"N.B. It must be observed that the above subjects are not expected to be treated Mathematically. Mathematical symbols may be employed so far as they express laws and results with precision, but Mathematical reasonings belong to the School of Mathematics."
Moreover the 1849 statute made no mention of practical work. This was introduced in a new statute in 1857, and gradually the classical content of the course was whittled away. A further statute in 1871 brought science degrees into something like their modern form.
At Cambridge an examination in natural science was instituted in 1851, but it did not bring a degree until 1861, twelve years after Oxford.
The reforms in Oxford were undoubtedly accelerated by the Royal Commission on the Universities of 1850. They proposed that a new university examination should be imposed at Oxford before matriculation and that proficiency in mathematics might compensate for failure in Latin (a recommendation which was adopted just over 100 years later!). They also proposed that a School of Mathematics and Physical Science should be established with two departments: (1) Pure and Applied Mathematics, (2) Mechanical Philosophy, Chemistry and Physiology together with all the Sciences subordinate to these three.
The report on Oxford was published in May 1852. A committee was appointed by the Hebdomadal Board to consider the recommendations and this reported in the following December. Its authors feared that `the Recommendations, if adopted as a whole, would prove revolutionary in character and disastrous to Discipline, Studies and Religion'. In spite of these reactionary sentiments, reforms came steadily.
In the second half of the 19th Century there were two outstanding mathematicians at Oxford:
Henry Smith (1826-83) was educated at Balliol and was Savilian Professor of Geometry from 1861 until his death. He did brilliant work in the theory of numbers and was awarded posthumously by the Academie Francaise their Grand prix (shared with Minkowski) for completing the work of Eisenstein on the representation of numbers by the sum of five squares. Actually Smith had gone on from five squares to seven squares and had published all the results 14 years earlier! The French had failed to notice that their problem was already solved.
J.J. Sylvester (1814-97) was appointed Savilian Professor on the death of Henry Smith. He was 69 at the time! His life story has been admirably told in Men of Mathematics by E.T. Bell (3) and I shall not risk spoiling it. It is enough to say that his election to the Savilian Chair was the first recognition of his genius that Sylvester had had from a British University. Mathematical honours had come his way but no suitable university post. It brought him to Oxford agog with a new mathematical theory - that of differential invariants - and he gave his inaugural lecture on the subject and embellished it with a poem. (The theory of versification was one of his major interests).
Sylvester's yeass at Oxford were the happiest that he spent in Britain and it is due to this fact that the Mathematical Institute now possesses Sylvester's own copy of his Laws of Verse bound together with his presidential address to the Mathematical Association. This small book was found by Professor G.N. Watson in a tray of sixpenny books. He recognised it as Sylvester's own copy from the marginal annotations and he decided that it should find a permanent home where Sylvester had been happiest.
V
Since 1900
The 20th Century has seen the enormous growth of mathematics and science at Oxford. The first increase in the number of professors of mathematics occurred in 1892 when four Waynflete chairs, one being for Pure Mathematics, were established at Magdalen in lieu of the three Praelectorships mentioned in its ancient statutes. In 1928 the Rouse Ball Chair for Applied Mathematics was established at Wadham bringing (with the Sedleian Chair) the number of chairs for applied mathematics up to parity with the number for pure mathematics Since World War II, chairs for Numerical Analysis, Mathematica1 Logic, Biomathematics, Mathematics, Mathematics (Theory of Plasma) and Computation have been created.
Of the eminent holders of mathematical chairs (restricting myself to those who are no longer alive), I can only refer in any detail to two, chosen for their influence on mathematics both in Oxford and in the world. The first is G.H. Hardy (1877-1947), who came to Oxford in 1920 from Trinity College Cambridge when he was elected Savilian Professor of Geometry. He occupied the chair for eleven years, after which he returned to Cambridge as Sadleirian Professor. The second is J.H.C. Whitehead (1905-1960) (always called "Henry"), who had been at Balliol as an undergraduate and as Tutorial Fellow. He was elected Waynflete Professor in 1947 and he occupied the chair for thirteen years. Each was appointed immediately after a world war when the ablest students surviving from the war years were entering or returning to Oxford. Each was the right man in the right place at the right time. Hardy founded a school of analysis in Oxford and his work was carried on by his pupils, foremost among whom was E.C. Titchmarsh (1899-1962), who succeeded Hardy as Savilian Professor in 1931. Henry Whitehead founded a school of topology in Oxford, which attracted pupils from all over the world.
Hardy was the author or co-author of about 10 books and more than 300 original papers of which 100 were published during his eleven years in Oxford. He was the most eminent British pure mathematician of the first half of this century. His papers have been collected and edited and they are being published in seven volumes. Anyone wishing to know more of Hardy's life should read the excellent obituary written by Titchmarsh, which has been reprinted at the beginning of Vol. I. In a sense I am a mathematical grand-daughter of Hardy, as I was supervised by two of his Oxford pupils, L.S. Bosanquet in London and Titchmarsh in Oxford. I only met the great man once and then he was external examiner for the London M.Sc. degree. Three of us were candidates. Hardy had a passion for cricket and the vivas had to be arranged to coincide with a good match at Lords. My viva was one of the grimmest experiences of my life, though I know that it had a salutary effect. The experiences of the other two were similar. We all passed, but in memory I can still see Hardy, stretched out in a deep and low armchair, pulling my dissertation to pieces!
Henry Whitehead was one of the most human mathematicians that we have ever had at Oxford. He took a tremendous interest in everyone around him, and he always wanted to hear about your mathematics and not just to tell you about his own. He helped to make the Mathematica1 Institute at Oxford one of the happiest of all university departments, and his zest for life, backed by his deep appreciation of the thoughts and feelings of the person to whom he was talking, made him friends all over the world. His contributions to geometry and topology were massive, but he is remembered with affection by many who never read his papers.
In choosing Hardy and Whitehead for more detailed discussion, I feel that I have neglected applied mathemdtics, where tribute should certainly have been paid to E.A. Milne (l896-l950), the first Rouse Bail Professor, whose reputation was more international than national. He was `one of the greatest figures in the greatest period of development of modern astrophysics and cosmology' (to quote from his Royal Society obituary). Moreover tribute must be paid to Milne's successor in the Rouse Ball Chair (1952), C.A. Coulson (1910-1974), through whose initiative this account of Oxford Mathematics and Mathematicians has been produced as a pamphlet. Charles Coulson was a man who packed into his life twice as much as any normal academic person. His interests in science and mathematics were combined in his research papers on Theoreticai Chemistry, of which Subject he became the first holder of a new chair (1972). He had a gift for lucid exposition and was constantly in demand as a lecturer both at home and overseas. He was, in fact, indefatigable in his work, not only for science and mathematics, but also on behalf of people, whether black or white, young or old. The following quotation from his first inaugural lecture (1952) sums up his own life and work as well as the spirit of applied mathematics as he saw it: `Applied mathematics is an intellectual adventure in which are combined creative imagination and authentic canons of beauty and fitness; they combine to give us insight into the nature of that world of which we ourselves, and our minds, are part'.
These words of Charles Coulson bring applied mathematics, as well as pure, into line with the image of Oxford mathematics as seen by the music critic of The Times, who wrote in 1952
`At Redbrick they treat mathematics as an instrument of technology; at Cambridge they regard it as an ally of physics and an approach to philosophy; at Oxford they think of it as an art in itself having affinities with music and dancing'.
Even with diversifying branches of mathematics, this image of Oxford is still approximately true. It is only restrictions of space in the Mathematical Institute that separate the professors of Numerical Analysis, Computing and Biomathematics from their colleagues, and all branches are still treated as related aspects of one exciting subject which is studied for its own sake.
Bibliography
1. Ball, W.W.R. A Short Account of the History of Mathematics, Macmillan 1924.
2. Bell, E.T. Development of Mathematics, McGraw Hill 1945 (second edition).
3. Bell, E.T. Men of Mathematics, II. Penguin Books 1953 (first published 1937).
4. Birch, T. The Works of the Hon. Robert Boyle, VI 459, 1772 (second edition).
5. Crombie, A.C. Augustine to Galileo I, II. London 1961 (second edition).
6. Dingle, H. Edmond Halley, His time and ours. (Halley Lecture for 1956), The Observatory 76, 117-131, 1956.
7. Gunther, R.T. Early Science in Oxford, I, Part II - Mathematics. Oxford 1922.
8. Hardy, G.H. Collected Papers of G. H. Hardy, I. Oxford 1966.
9. Mallet, C.E. History of the University of Oxford, II, III. Methuen 1924-7.
10. Molland, A.G. The geometrical background to the "Merton School". British Journal for the History of Science IV, 108-125, 1968.
11. Plot, R. The Natural History of Oxfordshire, 280-1. 1705 (second edition).
12. Purver, M. and Bowen, E.J. The Beginning of the Royal Society. Oxford 1960.
13. Ronan, C.A. Edmond Halley. Macdonald, 1970.
14. Sherwood Taylor, F. The teaching of science at Oxford in the nineteenth century. Annals of Science 8, 82-112, 1952.
15. Talbot, C.H. Simon Bredon (c. 1300-1372), Physician, Mathematician and Astronomer. British Journal for the History of Science I, 19-30, 1962.


