EVENTS
Friday 9th September, 10:00 - 19:00, Workshop
Expert discussion of items from Oxford's collections and their broader context: registration details here https://visit.bodleian.ox.ac.uk/event/sep22/imagining-ai-a-view-from-the-archive
The event will be chaired by Professor Ursula Martin of Wadham College and Oxford Mathematics. Speakers include:
- Troy Astarte (Swansea) on Christopher Strachey's 1950s experiments with computer poetry and chess
- David Brock (Computer History Museum, Mountain View) on the curation of AI experiments
- Kanta Dihal (Cambridge), editor AI Narratives (2020, OUP) and Imagining AI (2023, OUP)
- Sharon Ruston (Lancaster) author of “The science of life and death in Frankenstein" (Bodleian)
- Máté Szabó (Oxford, Greenwich) on "Max Newman's influence on Turing's early work"
A panel discussion chaired by Professor Rob Iliffe, Head of the Faculty of History, will explore how the history and philosophy of AI and computing can enrich contemporary conversations about the use of these transformative technologies.
See titles, abstracts and more about our speakers here.
Saturday 10 September, Imagining AI demonstrations with Oxford Open Doors
Encounter a world of AI at the Weston Library.
Meet Ai-Da – booking essential, 11.00 – 12.00 Sir Victor Blank Lecture Theatre Meet Ai-Da, the world’s first ultra-realistic robot artist, for a Q&A and live art session hosted by Cheney School’s Rumble Museum Council students. If you have a question for Ai-Da please send it to @email by Friday 27 August with the subject line ‘Question for Ai-Da’. More here
Encounter AI – drop-in 10.30 – 15.30 Blackwell Hall.
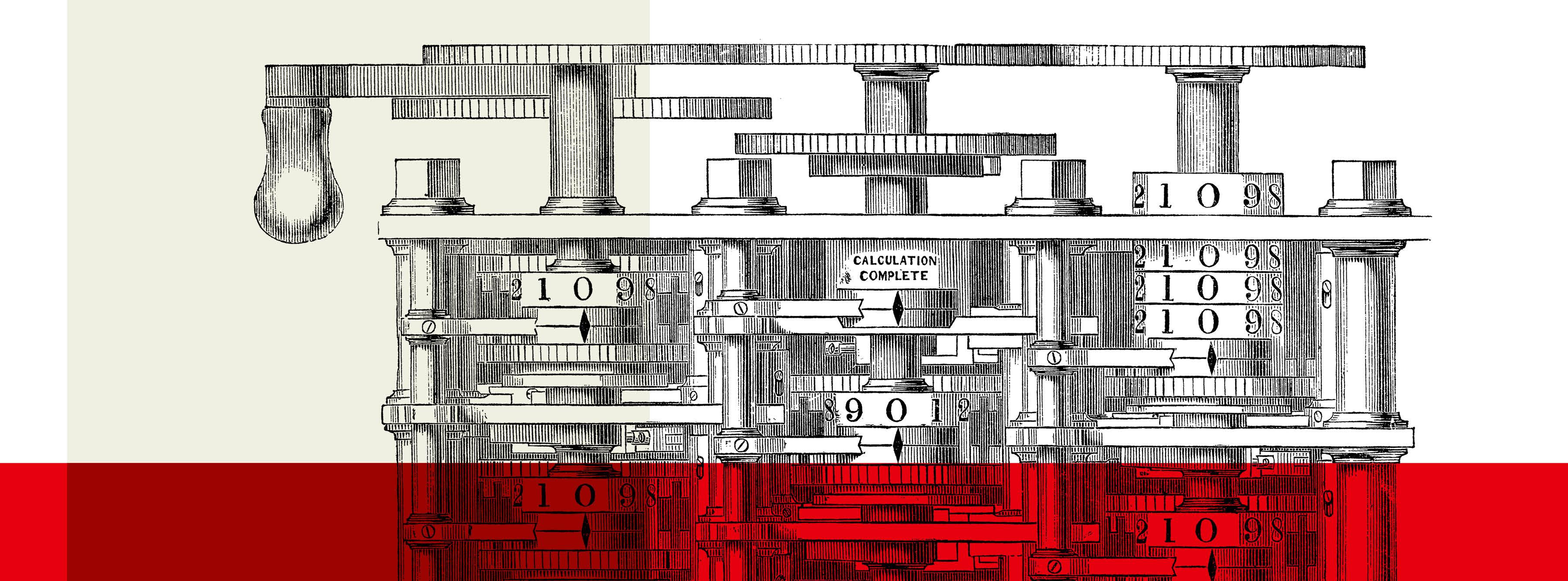
- See a demonstration of a Difference Engine in action, inspired by Charles Babbage's work, courtesy of Royal Holloway, University of London. More here.
- Discover a cybernetic ladybug that responds to light, sound and interaction. This model provided courtesy of the John von Neumann Computer Society is based on the Hungarian original from the late 1950s. More here.
- Students from Cheney School will exhibit artwork and creative writing responding to artificial intelligence in our lives today and in the future.
- Ai-Da will be in Blackwell Hall 13.30 – 15.30 for photographs only.
DISPLAYS OPENING 9th SEPTEMBER
Blackwell Hall, Weston Library Explore the ideas that led to contemporary AI with manuscripts of computer pioneer Ada Lovelace; pages from Mary Shelley's draft of "Frankenstein", and notes on computer poetry and draughts from Turing's collaborator Christopher Strachey. The History of Science Museum are lending Stanley Jevons's remarkable mechanical “reasoning piano” from the 1860s, and an even earlier pocket logic calculator.
History of Science Museum See the earliest plans and prototypes of Charles Babbage's computers, and Ada Lovelace's so-called "first programme".
OTHER
13th June and afterwards online, Meet the machines Sharon Ruston and Ursula Martin take a closer look at manuscripts of Mary Shelley, Humphry Davy and Ada Lovelace. Online link to follow.
cs4fn magazine Cunning Computational Contraptions: Issue 28 of the cs4fn magazine from Queen Mary University of London looks at some of the machines contrived in earlier times to support dreams of artificial intelligence.
The project acknowledges support from UKRI, Oxford's Faulty of History and Mathematical Institute, Wadham College Oxford and the HAPOC Commission. With thanks to David Dunning, Máté Szabó, Colin Williams and colleagues at the Bodleian Libraries, History of Science Museum, Oxford History and Oxford Mathematics.
Friday 9th September, 09.30-17.30, Workshop, Further details
09.30 Register, Blackwell Hall Cafe open.
10.00 Welcome and introduction. Professor Ursula Martin, Wadham College Oxford and Oxford Mathematics
10.10 Professor Sharon Ruston, ‘Minds and Machines in Mary Shelley’s Frankenstein and beyond’
Abstract: The question of whether the Creature in Frankenstein is human is one that continues to be asked. Is he more like a man or a machine? In what ways is he like or like us? How much humanity does his maker, Victor Frankenstein, demonstrate in the novel? In this talk, I’ll consider how Mary Shelley’s novel discusses concepts such as the mind, morality, and the soul. I’ll look at other literary examples of apparently mindless states of being, such as suspended animation, somnambulism, and automata. I will also examine some unpublished manuscript notebook pages of the young Davy as he reflects on the dangerous idea that the mind might be thought of as merely a thinking machine. A page of Mary Shelley's manuscript can be seen in the accompanying display.
Biography: Professor Ruston is Chair in Romanticism at Lancaster University. She has published The Science of Life and Death in Frankenstein (2021), Creating Romanticism (2013), Romanticism: An Introduction (2010), and Shelley and Vitality (2005). She co-edited the Collected Letters of Sir Humphry Davy for Oxford University Press (2020). She currently leads an AHRC-funded project to transcribe all of the notebooks of Sir Humphry Davy (and urges everyone to help with this task!), details are here: Davy Notebooks Project | Zooniverse - People-powered research.
10.50 Dr David E Dunning, "A Purely Mechanical Form”: William Stanley Jevons and the Materiality of Reasoning
Abstract: In the 1860s, philosopher of science and political economist William Stanley Jevons (1835–1882) designed a Logic Machine that, he claimed, reduced deduction “to a purely mechanical form.” As a box with a keyboard that mechanically spits out solutions to problems input by a user, this Logical Piano (as it is also known) readily evokes an embryonic idea of the digital computer when viewed with modern eyes. But perhaps what links this device most profoundly to today's computers is, ironically, the fact that it was not really about computing. While the digital computer’s better known predecessors (such as Babbage’s engines) were concerned with numerical calculation, Jevons pursued a more philosophical goal, aiming to show that reasoning was a fundamentally material process. Like the notions of AI that emerged in the second of half of the twentieth century, his project envisioned a form of computing far more expansive than number crunching. In this talk I will situate Jevons’s machine in the context of early symbolic logic that produced it, focusing on the novel techniques of writing that he built on, and built into his device. I will use this history to understand the role of material processes such as instruction, display, and memory in the context of machines and the intelligence we imagine them to possess. The machine can be seen in the accompanying display.
Biography: David E. Dunning is a Lecturer in the Integrated Studies Program at the University of Pennsylvania and the 2022–23 IEEE Life Member History Fellow. He is a historian of science, technology, and mathematics, whose research focuses on the material and social dimensions of abstract knowledge. He co-developed the Imagining AI display while at the Mathematical Institute at the University of Oxford.
11.30 David C. Brock, Learning from AI’s Eternal Recurrence: Documenting the History of Expert Systems at the Computer History Museum
Abstract: The starting point for some of the Computer History Museum’s most recent work to document the history of artificial intelligence – through proactive collecting and oral histories – was recognizing a striking recurrence of both rhetoric and action in and around the artificial intelligence community. Increasingly over the past decade, researchers and commentators alike have hailed the combination of neural networks with large data sets and vast amounts of computing resources as a fundamental break with the past, with transformative sociopolitical implications for the near and far futures. The current CEO of Google recently went so far as to compare this to the first human control of fire. This same rhetoric – and the same flurry of action spanning commercialization and expanded government, especially military, interest and investment – can be found in the artificial intelligence community and commentators of the 1980s. Then, the past-shattering and future-altering combination was expert systems and advanced computing resources. In this talk, I will attempt to elucidate this recurrence, and will argue that one of the most celebrated achievements of the expert systems era – the military logistics system, DART, deployed by the US in the Gulf War of 1990-1991 – shows one possible future for our current moment.
Biography: David C. Brock is the Director of Curatorial Affairs, and the Director of the Software History Center, for the Computer History Museum in Mountain View, California. He is the co-author of Moore’s Law: The Life of Gordon Moore, Silicon Valley’s Quiet Revolutionary (Basic Books, 2015) and of Makers of the Microchip: A Documentary History of Fairchild Semiconductor (MIT Press, 2010).
12.10 Break Lunch can be purchased in the Blackwell Hall Cafe, or elsewhere. Dedicated seating available.
13.30 Dr Troy Astarte, Christopher Strachey and the “thinking” machine
Abstract: As the electronic calculator of the 1940s was replaced by the computer of the 1950s, and its flexibility was slowly revealed, comparisons to human cognition were immediate: Giant Brains and Faster than Thought. While most who worked with computers knew this was little but a metaphor, the question of whether machines could really think was a good route for exploring their capabilities. This was certainly the case for Christopher Strachey (1916–1975), with a Bloomsbury Group pedigree and protean curiosity. In 1950, he was a schoolmaster at Harrow, but managed to find himself time to experiment with computers. While most computer applications were still numerical, Strachey explored games, literature, and music, alongside systems to make programming easier. These various programs, some of them almost unique in their time, gave Strachey ample opportunity to ruminate on the question of computers and their ability to think—or lack thereof. Strachey's notes can be seen in the accompanying display.
Biography: Troy Kaighin Astarte is a teaching-focused lecturer in computer science at Swansea University. Educated in computing at Newcastle University, their research interest moved to the history of computing and computer science in particular. Building on research on the history of formal semantics of programming languages, and the history of concurrency, Troy is interested in questions about the role of computer science in shaping the world and vice-versa.
14.10 Dr Máté Szabó, Max Newman's Influence on Turing's Early Work
Abstract: In 1936 Turing published his groundbreaking article “On Computable Numbers”, in which he described a mathematical model of machine computation that later became known as Turing Machines. Turing became interested in the topic while attending Max Newman’s course on logic and foundations of mathematics a year earlier. In this talk I will take a look at little known early works of Newman and show how they ifluenced Turing’s seminal paper.
Biography: Máté Szabó is a historian and philosopher of computing and mathematical logic. He earned his PhD in "Logic, Computation and Methodology" from the Department of Philosophy at Carnegie Mellon University. He co-developed the Imagining AI display while at the Mathematical Institute at the University of Oxford, and is currently he is a lecturer at the University of Greenwich.
14.50 Dr Kanta Dihal, How the world sees intelligent machines
Abstract: People have been imagining intelligent machines for millennia, in ways that vary greatly across cultures. Yet as artificial intelligence begins to fulfil its potential as a technology, spreading across the globe from its origins in 1950s America, many of these perspectives are marginalised. These stories, films, and visions matter: they are entangled in broader cultural attitudes and approaches to AI, reflecting or inspiring, embedding or disputing them. I will introduce such visions from across the globe, and what they can tell us now that AI is becoming a technological reality. I will draw out three themes: real and apparent differences between ‘Eastern’ and ‘Western’ portrayals of AI; visions of AI in communist states; and narratives of AI that explicitly aim to reject colonialist views of the technology.
Biography: Dr Kanta Dihal is a Senior Research Fellow at the Leverhulme Centre for the Future of Intelligence, University of Cambridge. Her research focuses on science narratives, particularly those that emerge from conflict. She currently manages the project ‘Desirable Digitalisation’, an international research collaboration that investigates intercultural perspectives on AI and fundamental rights and values. She is co-editor of the books AI Narratives (2020) and Imagining AI (2023) and has advised the World Economic Forum, the UK House of Lords, and the United Nations. She obtained her DPhil on the communication of quantum physics at Oxford in 2018.
15.30 Break, refreshments can be purchased at the cafe. Dedicated seating available.
16.00 Panel discussion hosted by the Faculty of History The panel will explore how the history and philosophy of AI and computing can enrich contemporary conversations about the use of these transformative technologies.
Chair: Professor Rob Iliffe, Head of Oxford's Faculty of History Panellists: Al Brown, Visiting Fellow, University of Oxford.; Dr Keith Dear, Defence & National Security, Fujitsu; Dr Kanta Dihal, University of Cambridge; Dr Philip Garnett, University of York; Professor Sharon Ruston, University of Lancaster; Dr Keith Scott, De Montfort University; Colin Williams, University of Oxford.
17.30 - 19.00 Reception: wine, soft drinks and snacks.








