Adaptive Cancer Therapy: tackling cancer drug resistance by capitalising on competition

How to deal with resistance? This is the headline question these days with regards to COVID vaccines. But it is an important question also in cancer therapy. Over the past century, oncology has come a long way, but all too often cancers still recur due to the emergence of drug-resistant tumour cells. How to tackle these cells is one of the key questions in cancer research. The main strategy so far has been the development of new drugs to which the resistant cells are still sensitive. While this approach has been successful, it often doesn’t take too long for further mutants to arise, requiring yet another set of new treatments.

About ten years ago, a group at the Moffitt Cancer Center in Florida proposed that, alternatively, it may be possible to fight resistance through a change in treatment scheduling. Tumours are complex ecosystems in which cancer cells compete with each other for limited space and resources. The researchers hypothesised that it may be possible to leverage this competition to suppress the growth of resistant cells.

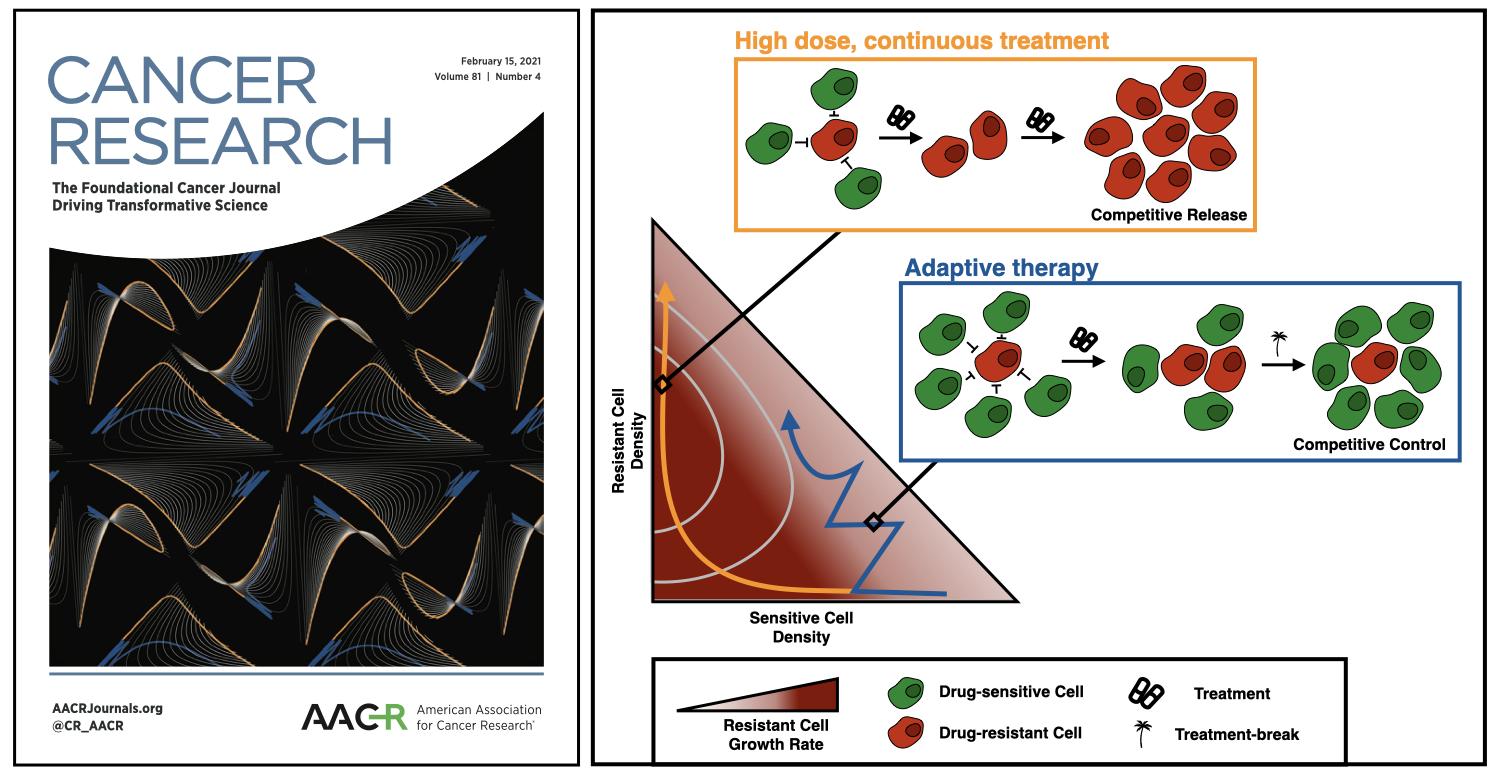
Cancer drugs are typically given so as to maximise the tumour cell kill. However, this quickly releases any surviving resistant cells from intra-tumoral competition, allowing them to proliferate (Figure 1). Instead, the researchers proposed “adaptive therapy” in which treatment is reduced once the tumour burden has been brought down to a tolerable level. In this way a pool of sensitive cells is maintained which will competitively suppress the resistant cells (Figure 1). This idea was inspired by similar approaches which are used in the management of pesticide resistance and invasive species, and was supported by prior mathematical modelling studies carried out, for example, at the Wolfson Centre for Mathematical Biology (WCMB) in the Mathematical Institute in Oxford. Adaptive therapy has subsequently been developed further by the Integrated Mathematical Oncology (IMO) department at Moffitt (the first mathematics department in a Cancer centre), and has recently been successfully tested in a clinical trial in prostate cancer, where it achieved both a 10 month increase in the time to progression, as well as a 53% reduction in cumulative drug usage.

But what are the factors which determine whether or not adaptive therapy will be beneficial? Despite promising pre-clinical and clinical results, and a number of elegant modelling studies, these factors have remained unclear. Yet this knowledge is important, as there is growing interest in testing adaptive therapy also in other settings. One factor which has been a point of particular controversy was the so-called “cost of resistance”. This refers to the concept that as resistant cells have to divert energy towards mechanisms to deal with the drug (e.g. pumps that remove drug from the cell), they will proliferate more slowly in a drug-free environment, i.e. they will pay a fitness cost for their resistance trait. It is intuitive that such a cost will facilitate keeping resistant cells at bay, and this had been one of the key arguments for adaptive therapy in its original development. But is it required? For example, an experimental collaborator of ours at Moffitt found that he could detect such a cost, if he grew cells in low nutrient conditions, but not if he grew them in normal culture medium. Given this context dependence, can adaptive therapy still work even if resistant cells do not pay any cost?

To address this question, we, Maxi Strobl, a DPhil student in the Systems Approaches to Biomedical Science Doctoral Training Centre (SABS DTC) and Philip Maini (Oxford Mathematics) in collaboration with a team of theoreticians, clinicians and experimentalists at the IMO (Jeffrey West, Mehdi Damaghi, Mark Robertson-Tessi, Joel Brown, Robert Gatenby and Sandy Anderson) and mathematician Yannick Viossat (Universite Paris-Dauphine) analysed a simple ODE model. We assumed cells were either sensitive to treatment, or fully resistant, and that the two populations competed with each other in a Lotka-Volterra fashion. Subsequently, we compared two treatment protocols: i) continuous therapy at a constant, high dose, and ii) adaptive therapy, in which treatment is withdrawn upon a 50% burden reduction, and only reinstated when the tumour returns to its initial size (the algorithm used in the prostate cancer clinical trial). Using phase plane analysis we were able to show that adaptive therapy was beneficial under a wide range of conditions in our model.

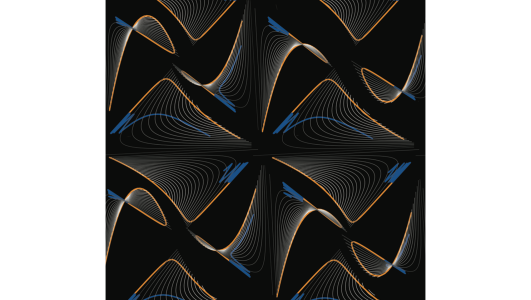
This result was not only comforting, but the phase planes allowed us to visualise our argument in a way that was more easily understandable to our biological and clinical collaborators. Essentially, we plotted the growth rate of the resistant cells as a function of the cell densities of the two populations, and superimposed the trajectories of the tumour during continuous or adaptive therapy. This shows quite nicely how, by maintaining more sensitive cells for longer, adaptive therapy stays in regions of smaller resistant cell growth than continuous therapy. In fact, an artistic collage in which we plotted these surfaces in 3-D (the third dimension being the resistant cell growth rate), was chosen for the cover image of the February 15th issue of Cancer Research in which our paper has appeared. Phase planes on the cover of one of the leading cancer research journals; what a great sign for the increasing role of mathematics in oncology (Figure 1)!

But what about resistance costs? To our surprise we found that costs seemed to have only a limited effect. They slowed disease progression, but did not change the relative benefit of adaptive therapy in our model. While this was a useful result, it was a bit puzzling. Costs might not always be necessary, but it seemed unlikely that they had such little impact. It turned out we had forgotten an important factor, which determines the actual “cost” of a resistance cost: the rate of cell death (also referred to as cell turnover). If this is small, then even a large cost is not a big problem, as the resistant cells can essentially just “hang out” until the tumour is (re)treated. However, if turnover is fast, then cells have much fewer opportunities to divide in their lifespan, so that every delay has an impact. In fact, this holds true not only for inhibition caused by resistance costs, but also for interference through competition.

We concluded that tumour cell turnover is an important, but so far overlooked, factor in adaptive therapy. Moreover, when we tested this by fitting our model to data from prostate cancer patients, we found a pattern which was indeed consistent with our hypothesis: patients whose tumours progressed on treatment were characterised by smaller estimates for their values of resistance cost compared to those patients who did not progress and who had a similar estimated rate of turnover (As a side note: interestingly, including an explicit death term can fix a number of problems of the logistic growth model and the Lotka-Volterra model more generally. If you’re interested to learn more, check out this blog post).

So what? Our work contributes to the theoretical understanding of adaptive therapy, and our insights on the role of turnover have two important implications. Firstly, they indicate that turnover is a factor we should think about when interpreting results from experimental models, as cell death rates vary between the flask, the mouse, and the human. Secondly, our insights provide a potential route for improving adaptive therapy by modulating cell death rates by using several drugs. Intriguingly, resistance costs are also a controversial topic in agricultural pest research, which inspired adaptive therapy. Yet despite the uncertainty about costs, pest management schemes have been effective by virtue of combining multiple interventions. How to choose and time combination treatment is a complex question but we believe that, again, integrating biology and mathematics will help us find the answer.

Figure 1: Using phase planes to visualise the mathematics of adaptive therapy. Left: Our collage of phase planes which made the cover of Cancer Research. Shown are an arrangement of different parameterisations as well as different viewing angles. Right: The underlying mathematics. Plotting the growth rate of the resistant cells we see that continuous high-dose treatment quickly removes all sensitive cells, resulting in rapid resistant cell expansion. In contrast, adaptative therapy maintains cell density high, which slows the growth of resistance by competitive suppression.