During the early growth of the brain, an extraordinary process takes place where axons, neurons, and nerves extend, grow, and connect to form an intricate network that will be used for all brain activities and cognitive processes. A fundamental scientific question is to understand the laws that these growing cells follow to find their correct target.
A well-known observation is that multiple axons bundle and migrate together towards other neurons to make connections, sometimes very far from the cells where they originate. During this trip, the tip of each axon can only rely upon its near environment to find its path. For example, chemical guidance (chemotaxis) is a major modality of axon navigation: when a "smell" is sensed, the axon tip pulls itself on the substrate to move and elongate the trailing axon towards or away from the signal (1).
Recently, it has been demonstrated that the mechanical environment (stiff or soft) is also critical. In particular, the ability of an axon to progress depends on the stiffness of the substrate (2), potentially allowing for durotaxis, i.e., migration along stiffness gradients (3). In a recent paper published in Phys. Rev. Lett, Oxford Mathematicians Hadrien Oliveri and Alain Goriely in a joint work with neurophysicist Kristian Franze found a surprising connection between classic optic ray theory and axonal migration.
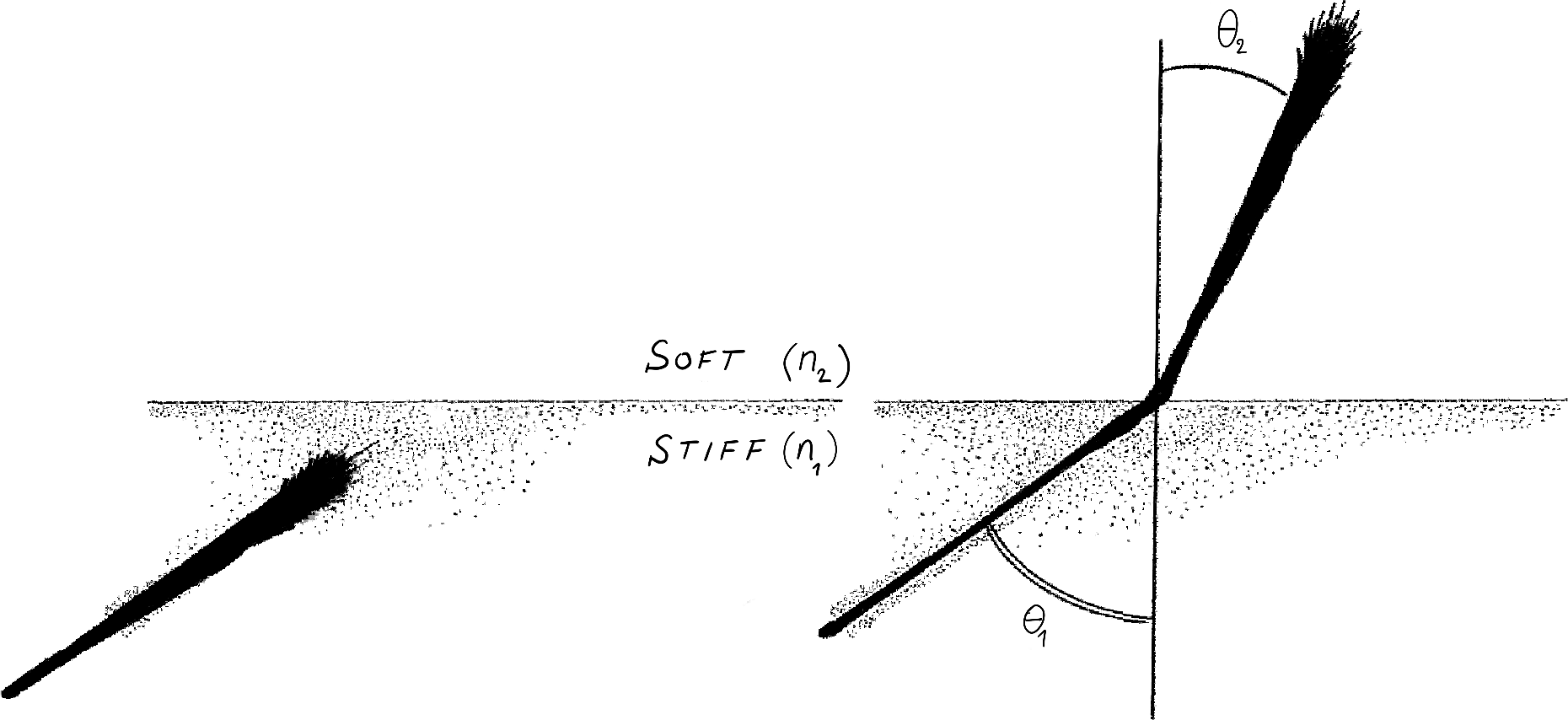
They started with the simple question: if each axon feels the stiffness of the substrate, what will be the overall group behaviour of the bundle? What path will a bundle follow if each axon produces a different force, depending on medium stiffness? Working in the theory of growing filaments (4), they modelled the path of a tip-growing bundle subject to differential traction forces. Then, they considered an idealised system where a bundle moves from a soft to a hard medium. In each separate domain the bundle follows a straight trajectory. However, when the axons approach the interface (say with incident angle $\theta_1$) part of the bundle will grow on the hard domain, while some axons are still on the soft domain. This results in a torque that forces the bundle to turn until all axons have passed the interface, at which point the bundle stops turning and follows a new straight trajectory ($\theta_2$, Fig 1).
FIgure 1: The Snell law of axon durotaxis.
The theory leads to a surprising relationship: $$ n_1 \sin\theta_1 \simeq n_2 \sin \theta_2 $$ where $n_i$ are related to the stiffness of each medium. The same mathematical relationship appears in a completely different setting. In optics, if $n_1$ and $n_2$ are the refractive indices and $\theta_1,\theta_2$ the angle that a light ray makes with the interface, this law is known as Snell's law (or Descartes's law in French). It governs the deflection of light rays at the interface between two refractive media (for example air and water) and is a consequence of Maxwell's equations for electromagnetic radiations. This law explains, for instance, why a wood stick appears broken when partially submerged in water.
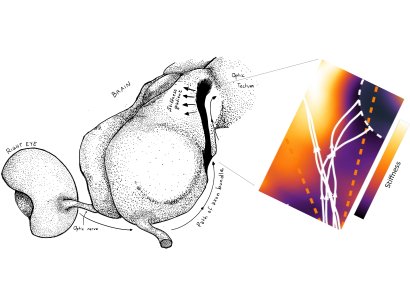
Using this theory, the authors showed how durotaxis can be used to explain the guidance of xenopus retinal ganglion cell axons, originated in the retina (3, Fig 2).
This analogy between the path of a light ray and the path of axons in the developing brain is potentially powerful. Indeed, we know from the theory of optics that ingenious devices such as lenses, mirrors, optical guides, collimators, binoculars, periscopes, telescopes and microscopes can be built to control the path of light rays and collect information. Similarly, the authors show how one can design substrate with different stiffness that would induce lensing effects, or create the equivalent of an optic fibre with a soft corridor to guide axons during development or during regeneration. Their new work provides a foundation for a general theory of axon guidance and control.
Figure 2: the role of tissue stiffness in Xenopus lævis visual system development. Left: cartoon showing the path of the axons from the retina, through the optic nerve to the optic tectum. Right: numerical simulation of retinal ganglion cell axons undergoing a sharp caudal turn at their arrival in the mid-diencephalon ($N=5$ representative trajectories). The authors show how durotaxis has the potential to contribute to this turn.
References:
1] K. Franze, “Integrating Chemistry and Mechanics: The Forces Driving Axon Growth,” Annual Review of Cell and Developmental Biology, vol. 36, Oct 2020.
[2] C. E. Chan and D. J. Odde, “Traction dynamics of filopodia on compliant substrates,” Science, vol. 322, pp. 1687–1691, Dec 2008.
[3] D. E. Koser, A. J. Thompson, S. K. Foster, A. Dwivedy, E. K. Pillai, G. K. Sheridan, H. Svoboda, M. Viana, L. da Fontoura Costa, J. Guck, C. E. Holt, and K. Franze, “Mechanosensing is critical for axon growth in the developing brain,” Nature neuroscience, vol. 19, no. 12, p. 1592, 2016.
[4] D. E. Moulton, T. Lessinnes, and A. Goriely, “Morphoelastic rods. Part I: A single growing elastic rod,” Journal of the Mechanics and Physics of Solids, vol. 61, pp. 398–427, Feb 2013.