Trigonometry - 2021

Part of the Oxford MAT Livestream

Download PDF version

MAT syllabus

Solution of simple trigonometric equations. The identities
$$\begin{equation*} \tan x = \frac{\sin x}{\cos x} ,\quad \sin^2 x + \cos^2 x = 1, \quad \sin\left(90^\circ - x\right) = \cos x. \end{equation*}$$
Periodicity of sine, cosine and tangent. Sine and cosine rules for triangles.

Revision

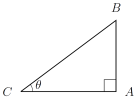
• If triangle $ABC$ is right-angled at $A$ and $\angle BCA=\theta$, then $$\sin\theta=\frac{|AB|}{|BC|}, \qquad \cos \theta=\frac{|AC|}{|BC|},\qquad \tan\theta=\frac{|AB|}{|AC|}.$$
• So $\displaystyle \tan\theta=\frac{\sin\theta}{\cos\theta}$.
• Also, by Pythagoras' Theorem, $|AB|^2+|AC|^2=|BC|^2$ so $\sin^2\theta+\cos^2\theta=1$.
• Since the angles in a triangle add up to $180^\circ$, the angle at $B$ is $90^\circ-\theta$.
  So $\sin(90^\circ-\theta)=\cos\theta$ and $\cos(90^\circ-\theta)=\sin\theta$.
• The sine, cosine, and tangent functions are all periodic; $$\sin(x+360^\circ)=\sin x, \qquad \cos(x+360^\circ)=\cos x,\qquad \tan (x+180^\circ)=\tan x.$$
• Also, we have $\sin (-x)=-\sin x$, and $\cos(-x)=\cos(x)$.

Now consider a triangle that is not necessarily right-angled.

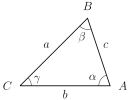
Let's write the angles at $A$, $B$, $C$ as $\alpha$, $\beta$, $\gamma$ respectively, and call the side-lengths $a=|BC|$, $b=|AC|$, $c=|AB|$.

• The area of this triangle is $\displaystyle \frac{1}{2}ab\sin\gamma$.
• (The cosine rule) We have $a^2=b^2+c^2-2bc\cos\alpha$.
• (The sine rule) We have $\displaystyle \frac{\sin \alpha}{a} = \frac{\sin \beta }{b} = \frac{\sin \gamma}{c}$.

Warm-up

• Write down the values of $\sin x$ and $\cos x$ and (where possible) $\tan x$ when $x$ is equal to $0^\circ$, $30^\circ$, $45^\circ$, $60^\circ$, $90^\circ$, $120^\circ$, $135^\circ$, $150^\circ$, $180^\circ$, $210^\circ$, $225^\circ$, $240^\circ$, $270^\circ$, $300^\circ$, $315^\circ$, $330^\circ$.
• Find all the solutions to $\displaystyle \sin x = \frac{1}{2}$ with $0\leq x < 360^\circ$.
• Find all the solutions to $\tan x = 1$ with $0\leq x < 360^\circ$.
• Find all the solutions to $\tan (45x) = 1$ with $0\leq x < 360^\circ$. [Careful, not just $1^\circ$ and $5^\circ$.]
• Simplify $\cos^4x+2\sin^2x\cos^2x+\sin^4 x$.
• For $0\leq x<90^\circ$, write $1-\sin^2 x+\sin^4 x-\sin^6 x+\dots$ as a single expression (not an infinite sum) in terms of $\cos x$. Why have I excluded $90^\circ$ from the range here?
• Write $\cos^4x+\cos^2x$ in terms of $\sin x$.
• Simplify $\cos(450^{\circ} -x)$.
• Simplify $\cos(90^\circ-x)\sin (180^\circ-x)-\sin(90^\circ-x)\cos(180^\circ -x)$.
  [If you know a fact about $\sin(A-B)$, you may only use it if you prove it!]
• A triangle $ABC$ has side lengths $AB=3$ and $BC=2$, and the angle $\angle ABC=120^\circ$. Find the remaining side length $AC$, the area of the triangle, and an expression for $\sin \angle BCA$.
• Write down three different expressions for the area of triangle $ABC$, with each expression involving two of the side-lengths and one of the angles. All of these expressions must be equal because they're all equal to the area. Divide each expression by the product of all three side-lengths and multiply by 2. Which rule have you arrived at?
• From the cosine rule, and the fact that $-1\leq \cos \alpha\leq 1$, deduce that for any triangle with side lengths $a>b>c>0$, we must have $a<b+c$ ("the longest side is shorter than the sum of the other two sides" or said differently "the shortest route from $B$ to $C$ is a straight line" also known as "the triangle inequality").
   

MAT questions

The minimum value achieved by the function
$$f(x)=9\cos ^{4}x-12\cos ^{2}x+7$$
equals

(a) 3,

(b) 4,

(c) 5,

(d) 6,

(e) 7.
 

Hint: you do not need to do any differentiation here!

MAT 2016 Q1D

How many solutions does $\cos^n(x) + \cos^{2n}(x) = 0$ have in the range $0 \leqslant x \leqslant 360^\circ$ for an integer $n \geqslant 1$?

(a) $1$ for all $n$,
(b) $2$ for all $n$,
(c) $3$ for all $n$,
(d) $2$ for even $n$ and $3$ for odd $n$,
(e) $3$ for even $n$ and $2$ for odd $n$.
 

Hint: the second term is the square of the first term.

MAT 2017 Q1F

The picture below shows the unit circle, where each point has coordinates $(\cos(x),\sin(x))$ for some $x$. Which of the marked arcs corresponds to 
$$\begin{equation*} \tan(x) < \cos(x) < \sin(x)\textrm{ ?} \end{equation*}$$

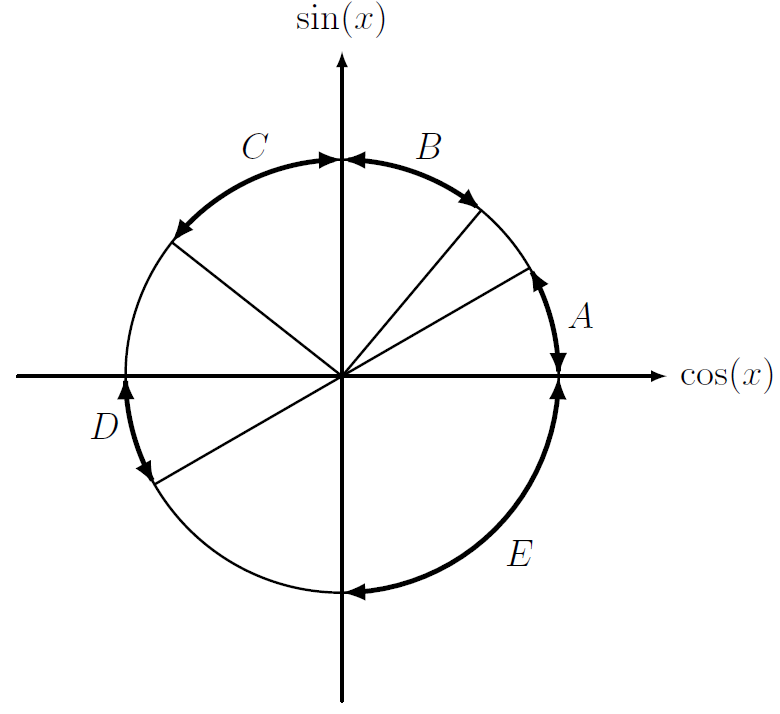
Hint: First, you could think about where $\sin x =\cos x$.

MAT 2013 Q4

(i) Let $a>0$. Sketch the graph of $$\frac{a+x}{a-x}\qquad \mbox{for}\quad -a<x<a.$$
    
(ii) Let $0<\theta<90^\circ$. In the diagram below is the half-disc given by $x^2+y^2\leq 1$ and $y\geq 0$. The shaded region $A$ consists of those points with $-\cos\theta\leq x\leq \sin \theta$. The region $B$ is the remainder of the half-disc. Find the area of $A$.

    
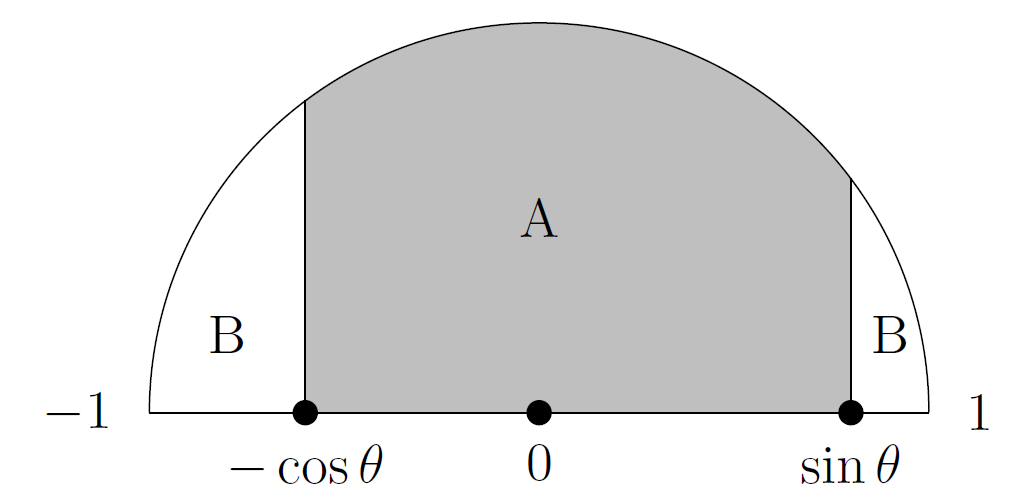
(iii) Assuming only that $\sin^2\theta+\cos^2\theta=1$, show that $\sin\theta\cos\theta\leq 1/2$.
    
(iv) What is the largest value that the ratio
     $$\frac{\mbox{area of } A}{\mbox{area of }B}$$
can be, as $\theta$ varies?
 

Hints: It's often helpful to draw in the radii when we've got a circle and we have some interesting points on the circumference. We're not actually given any angles in this question, but there is a $\theta$ here, so maybe we can find an angle that's $\theta$.

In part (iii) you may also assume that $x^2\geq 0$ for any real $x$.

Part (iv) actually relates back to the first part of the question, but perhaps you don't need to spot that in order to realise that you can make that ratio big just by making $A$ big.

Extension

The following material is included for your interest only, and not for MAT preparation.

Later in A-level Maths or equivalent, you will learn that if $y=\sin x$ then $\displaystyle \frac{\mathrm{d}y}{\mathrm{d}x}=\cos x$, and that if $y=\cos x$ then $\displaystyle \frac{\mathrm{d}y}{\mathrm{d}x}=-\sin x$. This means that we can draw a nice diagram where arrows represent differentiation, like this;

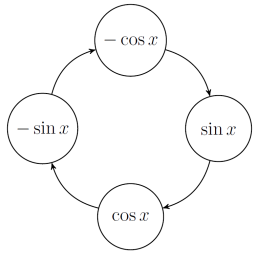
Even better, if you learn about complex numbers in Further Maths A-level or equivalent, then you'll find out about the number $i$ with $i^2=-1$. You already know that the derivative of $e^{kx}$ is $ke^{kx}$, so once you've seen complex numbers like $i$ then you can draw diagrams where arrows represent differentiation, like this;

So is $e^{ix}$ equal to $\sin x$? Well no, not quite. It behaves the same way as $\sin x$ when we differentiate it, but so does $\cos x$ or $3i\sin(x)$, so we've got options here. It turns out to be more useful to write $e^{ix}=\cos x + i\sin x$, which agrees with the values of $\sin x$ and $\cos x$ when $x=0$ (and, after differentiating, still agrees when $x=0$). This is known as "Euler's formula", but the English mathematician Roger Cotes knew it about twenty years earlier!