Many modern challenges facing industry and government relate to cleaning: removing pollution from water or industrial waste gases, or decontaminating the environment after chemical spills. Mathematicians in Oxford are collaborating with various industrial and government partners to model specific cleaning challenges, deepening understanding of these processes and working towards optimal cleaning solutions.
In this case study, we give an overview of three such collaborative projects that are currently ongoing. We conclude by reflecting on our approach to industrial applied mathematics and the mathematics of cleaning.
Removing microplastics: filtration in washing machines and tumble dryers
Microplastics are released from synthetic textiles during domestic washing and drying of clothing and, unless removed from the wastewater or air exhausts, these microplastics pollute the environment, with dangerous consequences for both wildlife and humans. Beko, a large manufacturer of washing machines and tumble dryers, is looking to improve the way that microplastics are collected in their device filters.
PhD student Torin Fastnedge (supervised by Chris Breward and Ian Griffiths) is working with Beko to study microplastic fibres in washing machines. He is investigating how the fibres are removed from clothing due to the shearing forces of fluid flowing over the textile. Torin is also modelling a new type of washing-machine filter, inspired by the gills of a manta ray, which concentrates the microplastic particles to enable more-efficient secondary filtration. A good understanding of the role of gill separation, angle, and fluid flow rate on particle capture is important to enable Beko to optimise their new filter design.
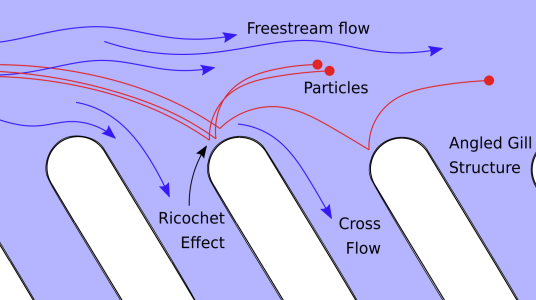
Schematic of a new filter design with angled “gills”: fluid passes between the gills but particles ricochet off and become more concentrated.
Meanwhile, master's student Chloe Bernard (supervised by Ian Griffiths and Colin Please) has investigated microplastic transport and capture in a tumble dryer filter, and the effect of microplastic-lint build up in the filter on the efficacy of the dryer as a whole.
Her hierarchy of models (from the bending of a single microplastic fibre, through the capture of particles within the filter, to the overall dryer system) has given insight into improved filter designs and operating regimes for the dryer, to maximise microplastic capture while also enhancing energy efficiency.
Efficient models for improving filter lifetime and efficiency
Filters are ubiquitous tools for cleaning gases and liquids, as in the previous example. W.L. Gore & Associates, Inc. (Gore) manufacture the membranes in many such filters, for use in domestic and commercial settings.
The deposition of particles within or on the surface of a filter membrane during its use eventually causes it to clog, resulting in decreased filter performance and downtime for replacement. Manufacturers such as Gore are broadly interested in extending filter lifetime (time until the membrane must be replaced) while maintaining a specified efficiency (proportion of particles removed from the fluid). They do this by tweaking membrane microscale properties such as the pore size-distribution and connectivity.
Filters are difficult to model in an accurate and efficient way because filtration is a spatially and temporally multiscale phenomenon. Particle trapping and the associated pore blocking on the microscale eventually cause overall filter clogging on the macroscale.
This only occurs once a large number of pores have been blocked, and so the trapping of a single particle occurs over a much shorter timescale than the lifetime of the filter. Modellers must therefore combine several length and time scales for a complete understanding of the filtration process.
During his PhD, Arkady Wey (supervised by Chris Breward, Jon Chapman and Ian Griffiths) has collaborated with Gore to develop models for filtration that carefully capture intricate couplings over multiple length and time scales, but are computationally efficient to simulate [1]. He has developed a 'size-structured model' to explore the effect of the pore size distribution: this captures the partial or complete blocking of pores with a distribution of sizes by particles with sizes drawn from another distribution.
Arkady has also developed a 'multiscale model' to capture the complicated pore connectivity, in which pore space is modelled as a network that is homogenised to arrive at a network-continuum multiscale system. This framework simultaneously captures microscale pore blocking and overall filter clogging, and careful systematic averaging means it is computationally efficient to solve on the filter scale.
Arkady's filtration models are useful tools for Gore to predict a filter's particle retention and lifetime. Their computational feasibility paves the way to filter optimisation, and may be used to address design questions such as “Given a desired particle retention efficiency and filter lifetime, what is the optimal size distribution and connectivity of the membrane pore space?”, ultimately improving filter performance.
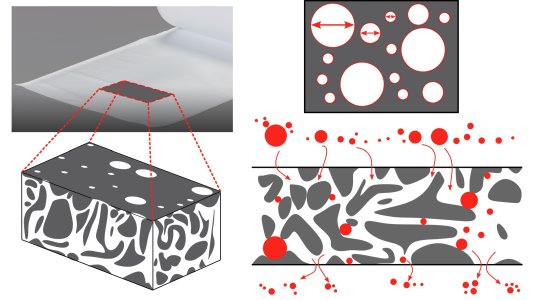
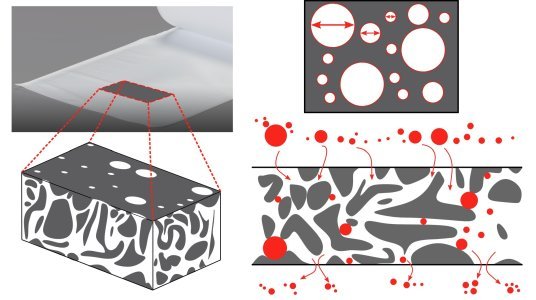
Illustrations of Arkady's size-structured model. (Left) The filter membrane modelled as a solid (grey) permeated by tunnels of pore space (white). (Right-Top) Top-view of a cross-section of the membrane. (Right-Bottom) Side-view of the membrane. Particles advect through pore space and deposit on pore walls.
Chemical weapons: decontaminating porous building materials
A separate cleaning problem is the decontamination of porous building materials. Following a chemical weapons attack, it is crucial for public safety that any hazardous chemical agent remaining in the environment is properly removed, which is especially difficult if it has seeped into porous building materials. A cleanser solution is typically applied to the surface, and allowed to react in, neutralising the hazardous agent in a chemical reaction. The cleanser and agent fluids are immiscible so the reaction takes place at the fluid-fluid interfaces within the pores of the material. Defra and DSTL are UK Government agencies with responsibility for the remediation in such scenarios, and must be able to decontaminate a site thoroughly, but as quickly and efficiently as possible.
Similar to the filtration problem above, the multi-scale nature of the decontamination process, with many moving chemical reaction fronts in the porespace, makes it difficult to simulate efficiently. Postdoctoral researcher Ellen Luckins (supervised by Chris Breward, Ian Griffiths, and Colin Please) has developed homogenised models for the decontamination dynamics, that accurately incorporate porescale chemistry while being computationally efficient to solve over the entire scale of the spill [2]. One particular difficulty is capturing the multi-scale nature of a sharp reaction front; this has been achieved using a combined homogenisation and boundary-layer analysis.
Analysis of these homogenised decontamination models has quantified the dependence of the decontamination time and the consumption of cleanser on parameters that Defra and DSTL can control such as the type and strength of applied cleanser, and the depth of the spill [3].
Additional recent work with Yibin Geng and Alissa Kamilova [4] has explored the effect of chemical contraction or expansion due to the reaction: expansion was shown to slow the decontamination, as the chemicals have to diffuse against the flow of material to reach the reaction front. Two current masters projects, sponsored by Defra/DSTL and supervised by Ellen Luckins and Yixuan Sun, are ongoing: Harvey Turner is investigating how best to apply cleanser in order to minimise wasted cleanser while retaining fast agent clean-up, and Aoibheann Murray is studying how to accurately detect whether agent is lurking unseen within porous building materials.
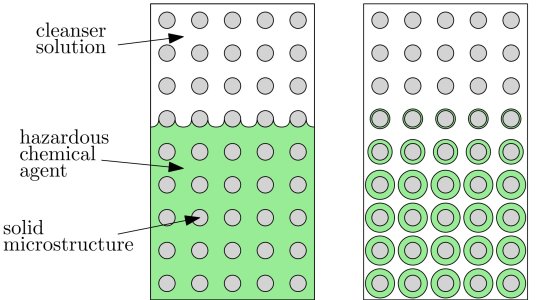
Illustrations of two decontamination scenarios, with hazardous chemical agent and cleanser interacting within a porous building material
Outlook
In all of these projects, we have collaborated with domain experts to deeply understand a real-world cleaning problem. We have then constructed mathematical models for the process, which have enabled us to understand the system behaviour more thoroughly, and to draw conclusions that are meaningful to the practical cleaning scenario.
We expect the application area of cleaning and decontamination to become increasingly important. As shown through the three examples in this case study, cleaning systems are complex and give rise to interesting mathematical questions. There are many wide-ranging opportunities for mathematical modellers to contribute to this field.
References
[1] A. Wey. Mathematical models of filtration. PhD thesis, University of Oxford, 2023.
[2] E. Luckins, C.J.W. Breward, I.M. Griffiths, and Z. Wilmott. Homogenisation problems in reactive decontamination. Eur. J. App. Math., 31(5):782–805, 2020.
[3] E.K. Luckins, C.J.W. Breward, I.M. Griffiths, and C.P. Please. The effect of pore-scale contaminant distribution on the reactive decontamination of porous media. Eur. J. App. Math., 2023 (in press).
[4] Y. Geng, A.A. Kamilova, and E.K. Luckins. Fluid-flow effects in the reactive decontamination of porous materials driven by chemical swelling or contraction. J. Eng. Math., 2023 (in press).